1022：Packing Unit 4D Cubes

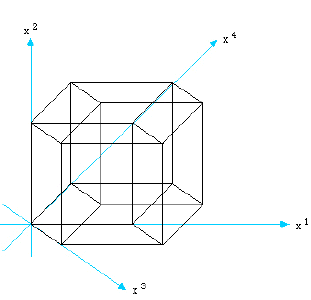
We usually think that there are three geometric dimensions; the fourth dimension is usually time. However, the Association for Customizing Machines (ACM) has to deal with four geometrical dimensions for their strange customer EE3 who needs to pack four dimensional products into perpendicular parallelepipeds before shipping them to the newly emerged market niche just on the outskirts of the Milky Way.
Each of EE3 products consists of a number of unit 4D cubes that are glued together at their faces. A face of a 4D cube is a 3D cube and each 4D cube has 8 such faces. The picture on the left shows a 4D cube projected into a plane with the four principal, orthogonal axes shown. It takes a bit of effort to stretch our imagination and see the faces of a 4D cube in such a projection. The pictures below try to illustrate how the two faces along each of the four axes are situated in 4D. Again, using just the planar projection it is not so easy to illustrate and takes some effort to see. But we have done a good job, didn't we?



Each EE3 product to be packed consists of a number of unit 4D cubes that are glued together along their faces which are 3D cubes. Your job is simple: find the minimal volume measured in the number of unit 4D cubes of a perpendicular parallelepiped (a 4D box) into which the product can be packed before shipping.

The first line of the input file contains a single integer t (1 ≤ t ≤ 10), the number of test cases, followed by input data for each test case describing one EE3 product. The first line of each test case is an integer n (1 ≤ n ≤ 100) which is the number of unit 4D cubes used in the product. Next, there are n lines, each describing one unit cube and contains 9 nonnegative integer numbers.
The first number, a positive integer, is the unique identifier of a cube and the remaining 8 numbers give the identities of neighbors of the cube listed in the following order:
?the first two numbers are identifiers of the cubes glued to the opposing sides of the given cube along the x1 axis as seen looking in the direction of the x1 axis;
?the next two numbers as above but for the x2 axis;
?the next two numbers as above but for the x3 axis;
?the next two numbers as above but for the x4 axis;
If a cube does not have a neighbor glued to one of its faces we use 0 instead of a cube identifier.
The problem is that the employees of ACM may produce inconsistent descriptions of EE3 products. There are two sources of such inconsistencies:
?A consistent description must be symmetric, i.e. if cube x is glued to cube y at some face then cube y must be glued to cube x at the corresponding face along the same axis. The following description is inconsistent:
3 0 0 1 0 0 0 0 0
1 0 0 3 0 0 0 0 0
?Any description must describe a single solid, i.e. there must be only one component in the product. Thus the following is inconsistent:
1 2 0 0 0 0 0 0 0
2 0 1 0 0 0 0 0 0
3 0 0 4 0 0 0 0 0
4 0 0 0 3 0 0 0 0

There should be one output line per test case containing either the number of unit 4D cubes in the smallest 4D perpendicular parallelepiped oriented along the axes into which the product can be packed if the description is consistent, or the word Inconsistent, otherwise.