7262：三角函数

进入初中后，小蒟蒻学会了四种神奇的三角函数：

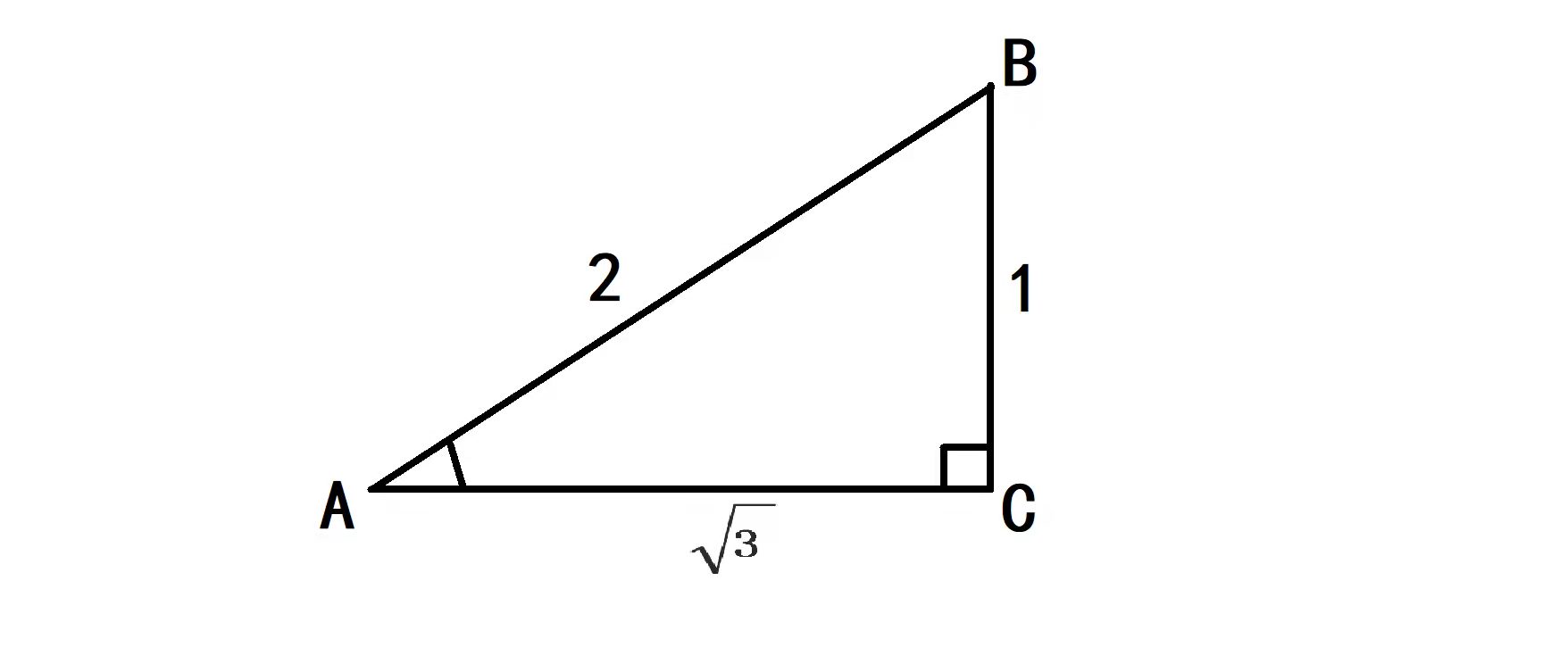
$\sin$：正弦函数，在直角三角形中，任意一锐角 $∠A$ 的对边与斜边的比叫做 $∠A$ 的正弦，记作 $\sin A$，比如在下图的三角形中 $\sin A = \frac{1}{2}$；

$\cos$：余弦函数，在直角三角形中，任意一锐角 $∠A$ 的邻边与斜边的比叫做 $∠A$ 的余弦，记作 $\cos A$，比如在下图的三角形中 $\cos A = \frac{\sqrt{3}}{2}$；

$\tan$：正切函数，在直角三角形中，任意一锐角 $∠A$ 的对边与邻边的比叫做 $∠A$ 的正切，记作 $\tan A$，比如在下图的三角形中 $\tan A = \frac{\sqrt{3}}{3}$；

$\arctan$：反正切函数，函数 $A = \tan B, B \in (-\frac{\pi}{2}, \frac{\pi}{2})$ 的反函数，记作 $B = \arctan A$。简单来说，$B = \arctan A$ 等价于 $A = \tan B$。



现在小蒟蒻手上有一个数 $m = 0$，每次操作它可以使用 $\sin$, $\cos$ 和 $\arctan$ 中的一个作用于 $m$ 得到 $m'$。小蒟蒻有一个幸运数字 $\sqrt{\frac{p}{q}}$ ，保证 $p \le q$ 且 $\gcd(p, q) = 1$。小蒟蒻想知道能否在 $2q$ 次操作内将 $m$ 从 $0$ 变到他的幸运数字呢？如果可以请输出其中任意一种方案，如果无解请输出 `Noooooooo!`。

为了简化方案的输出，我们记 $\sin$ 为 $s$， $\cos$ 为 $c$， $\arctan$ 为 $t$，输出的第 $i$ 个字符表示第 $i$ 次的操作类型。例如 $sct$ 表示 $\arctan(\cos(\sin(0)))$。

第一行一个整数 $T(1 \le T \le 10)$，表示数据组数。

对于每组数据，输入一行两个整数 $p$ 和 $q$。（$1 \le p \le q \le 10^6,\ \gcd(p, q) = 1$）

对于每组数据：

若有解，输出一行一个长度不超过 $2q$ 的字符串，表示答案；

若无解，输出一行一个字符串"`Noooooooo!`"（不含引号）。