7206：Planar graph

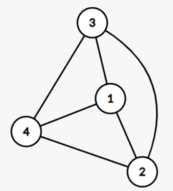
We say an undirected graph is a planar graph, if it exists a way to draw it on a planar, such that no two edges have intersection except the endpoint. For example, the graph below is a planar graph:

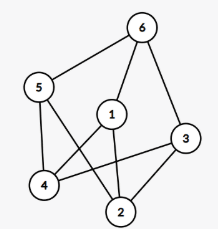
But this graph below is not a planar graph, since it can be proved that no matter how to draw this graph on a planar, at least two edges have intersection which is not an endpoint:

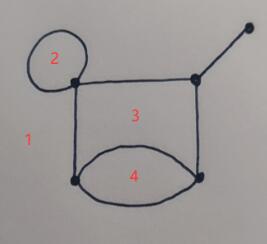
For a planar graph, it has some areas separated by edges. For example, the planar graph below has $4$ areas (Note that the area $1$ is the infinite planar outside):

Give you a planar graph with $n$ vertices and $m$ edges. Each area sets a country. You are the designer and you want to build some tunnels on the edges such that: From one city, you can travel to any other city by going through some tunnels or passing some cities(i.e. you can't cross one edge unless it sets a tunnel). For example, for the graph above, you can build tunnels like this:

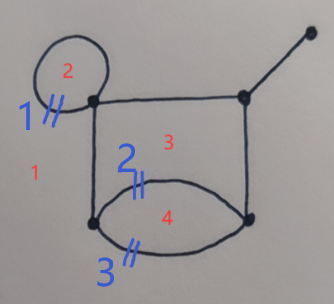
In the picture above, you can travel from city $2$ to city $3$ by going through tunnel $1$, passing the city $1$, then going through tunnel $3$, passing the city $4$, finally going through tunnel $2$, and you can arrive to city $3$. You can check that from any city you can travel to any other city.

You want the number of tunnels as small as possible. Print the minimum number of tunnels and the ID of edges you build tunnel on.

The first line contains one integer $T(1\le T\le 15)$, described the number of test cases.

For each test case:

The first line contains two integers $n, m(1\le n\le 10^5, 0\le m\le 2\times 10^5)$ separated by a space, described the number of vertices and edges.

Next $m$ lines, the $i$-th line contains two integers $u, v(1\le u,v\le n)$, separated by a space, described the endpoint of the $i$-th edge. The ID of the $i$-th edge is $i$.

It is guaranteed that the given graph is a planar graph. But this graph may have self-loop, parallel edge and the graph may not connected.

The output contains $2T$ lines.

For each test case:

The first line contains one integer $f$, described the minimum number of tunnels you have to build.

The second lines contains $f$ integers separated by spaces, the $i$-th integer described the ID of edges the $i$-th tunnel built on.

If for a fixed minimum number of tunnels, it has many ways to build the tunnels, print the lexicographically smallest answer.