7177：Link with Equilateral Triangle

Link has a big equilateral triangle with side length $n$. The big triangle consists of $n^2$ small equilateral triangles with side length $1$.

Link is going to fill numbers into each vertex of the small triangle with the following limits:

· The number filled in should be $0$, $1$, or $2$.
· The left side of the big triangle should not be filled with $0$. The right side of the big triangle should not be filled with $1$. The bottom side of the big triangle should not be filled with $2$.
· For each small triangle with side length $1$, the sum of three vertices should not be a multiple of $3$.



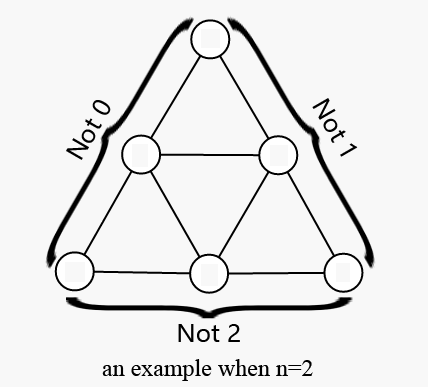
Link went crazy when he tried to do so because he couldn't find any triangle satisfying all conditions above. Now, he turns to you for help.

Please tell Link: Is it possible to fill the triangle so that it satisfies all conditions above?

Each test contains multiple test cases. The first line contains the number of test cases $T$ ($1 \le T \le 1000$). Description of the test cases follows.

For each test case, there is only one line containing a single integer $n$ ($1 \leq n \leq 10^3$).

For each test case, output ${\rm Yes}$ if it is possible to do so. Output ${\rm No}$ if it is impossible to do so.