当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
7120:Loneliness
Special Judge 特殊评判题目描述
The world that Kanari lives in is a grid of $n\times n$, and Kanari's home is on the top left corner $(1,1)$. One day, he decided to take an adventure to the bottom right corner $(n,n)$ of the world.
During the alone journey of Kanari, he feels lonely and he has 1 loneliness value at first. His sense of loneliness increases whenever he gets farther from home and decreases whenever he moves closer to it. To be specific, when he moves down, his loneliness value doubles; when he moves up, it halves; when he moves right, it is increased by 2 and when he moves left, it is decreased by 2.
More formally, let $(x,y)$ be the current position of Kanari.
Kanari can't move out of this world. At any time, his coordinate $(x,y)$ should satisfy that $1\leq x,y \leq n$.
In addition, to better perceive his loneliness, Kanari hopes that his loneliness value will always be a non-negative integer. That is to say, if Kanari's loneliness value is odd, he will not be able to move up; if Kanari's loneliness value is 1 or 0, he will not be able to move left.
Kanari hopes that when he reaches the bottom right corner, his loneliness value is $k$. When Kanari reaches the destination but his loneliness value is not $k$, he should continue to move. However, if Kanari's loneliness value exceeds $2k$ at any time, he will go crazy because he is too lonely, so he needs to avoid that.
If it takes Kanari too much time to settle down, he will also go crazy, so he hopes that he will not move more than 1000 times.
He wonders if he can find such a route, so he asks you for help. The route can be represented as a string consisting of "U, D, L, R". (U stands for up, D stands for down, L stands for left, R stands for right).
For example, if $n=4$ and $k=40$, Kanari can choose the route "RRDDLDRR".
His position and his loneliness value are as follows:
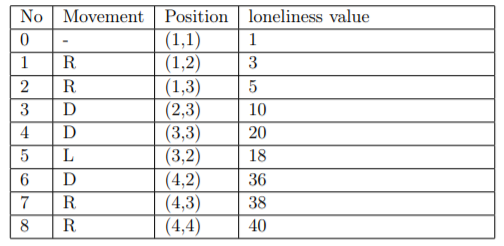
Pay attention: $n=4$ is just an example, the test data only contains the case of n = 100.
During the alone journey of Kanari, he feels lonely and he has 1 loneliness value at first. His sense of loneliness increases whenever he gets farther from home and decreases whenever he moves closer to it. To be specific, when he moves down, his loneliness value doubles; when he moves up, it halves; when he moves right, it is increased by 2 and when he moves left, it is decreased by 2.
More formally, let $(x,y)$ be the current position of Kanari.
- If he moves down, he moves from $(x,y)$ to $(x+1,y)$
- If he moves up, he moves from $(x,y)$ to $(x-1,y)$
- If he moves left, he moves from $(x,y)$ to $(x,y-1)$
- If he moves right, he moves from $(x,y)$ to $(x,y+1)$
Kanari can't move out of this world. At any time, his coordinate $(x,y)$ should satisfy that $1\leq x,y \leq n$.
In addition, to better perceive his loneliness, Kanari hopes that his loneliness value will always be a non-negative integer. That is to say, if Kanari's loneliness value is odd, he will not be able to move up; if Kanari's loneliness value is 1 or 0, he will not be able to move left.
Kanari hopes that when he reaches the bottom right corner, his loneliness value is $k$. When Kanari reaches the destination but his loneliness value is not $k$, he should continue to move. However, if Kanari's loneliness value exceeds $2k$ at any time, he will go crazy because he is too lonely, so he needs to avoid that.
If it takes Kanari too much time to settle down, he will also go crazy, so he hopes that he will not move more than 1000 times.
He wonders if he can find such a route, so he asks you for help. The route can be represented as a string consisting of "U, D, L, R". (U stands for up, D stands for down, L stands for left, R stands for right).
For example, if $n=4$ and $k=40$, Kanari can choose the route "RRDDLDRR".
His position and his loneliness value are as follows:

Pay attention: $n=4$ is just an example, the test data only contains the case of n = 100.
输入解释
The first line contains two integers $T,n$.($1\leq T\leq 10^4, n=100$)
Then $T$ lines follow, each line contains a single integer $k$. ($1\leq k\leq 10^{16}$)
In the sample, just to show the format, $T = 1, n = 4, k = 40 $, and your solution will not be tested using that sample. The first test is different from the first sample.
Then $T$ lines follow, each line contains a single integer $k$. ($1\leq k\leq 10^{16}$)
In the sample, just to show the format, $T = 1, n = 4, k = 40 $, and your solution will not be tested using that sample. The first test is different from the first sample.
输出解释
For each test case, if there is no route for Kanari to get to the bottom right corner, output -1, otherwise, output a UDLR string with length less than 1000 to represent the route.
输入样例
1 4 40
输出样例
RRDDLDRR
最后修改于 2021-10-23T19:11:34+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 262144/262144K(Java/Others) |
登陆或注册以提交代码