当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
7114:Cypher
题目描述
With the arrival of mechanical cryptography machines, cipher complexity exploded. A person enciphering or deciphering a message no longer needed to understand a cipher to use it, and messages which previously could take hours to encrypt were now enciphered almost instantly.
Lucida and Kanari were playing Counter-Strike: Global Offensive and needed frequent tactical exchanges. Losing interphone, they had to do radio communication, but the ease with which transmissions could be intercepted meant strong encryption became vital. They chose to adopt inventor Arthur Scherbius's Enigma machine, which was used by the German army during World War 2 and offered an unprecedented level of encryption.
When a letter key is pressed on the Enigma keyboard an electrical signal flows into a scrambler disc. This disc has 26 inputs and 26 outputs which are connected internally in a random fashion, so a signal entering at input $1$ may exit at output $14$. The signal passes through $n$ of these discs then is reflected so it passes back through the same $n$ discs again, before finally displaying the enciphered letter on a lampboard.
So far this is just a monoalphabetic substitution cipher, however, Enigma's strength comes from the fact that the discs rotate. The first disc rotates on every press, when it rotates a whole circle, it will cause the next disc to rotate and so the second will eventually cause the third disc to rotate and so on. This means the machine is a polyalphabetic cipher that can cycle through $26^n$ unique substitution alphabets before repeating.
To make the machine even more secure, up to 10 pairs of letters on the keyboard can be swapped using patch cables. Combined with the $26^n$ possible starting rotations for the scrambler discs the total number of initial configurations for the machine is large enough to avoid being deciphered.
As long as the machine is set to the correct initial setting it will decipher a message encrypted using the same settings, the initial setting is therefore the key. Lucida and Kanari used a new key for each game and sent out top-secret code books containing the initial Enigma settings every day. The Enigma worked well and they won most of the game by using the secret tactics.
Formally, the Enigma consists of three parts. They are combined with each other via signals. The signals indicate a location between $1$ to $26$, sometimes we may also use 'A' to 'Z' instead of $1$ to $26$ for convenience. When a key on the keyboard is pressed, there will be signals sent from the first part to the second part and then to the third part. After some process, signals will be sent back to the first part and finally become a letter shown on the lampboard.
The first part contains $p$ patch cables that can swap $p$ pairs of letters on the keyboard. It is guaranteed that the 2p letters are distinct. For example, if the letter 'A' and 'B' are swapped, after you pressed 'A', what's actually going into the second part is the signal of 'B'(2); when a signal of 'A'(1) comes from the second part, what's actually shown in front of you is letter 'B'.
The second part are $n$ discs which play the key role of the Enigma. Each disc can be seen as a monoalphabetic substitution cipher. Each disc has two rows up and down, and each row contains an 'A' to 'Z' permutation. Initially, letters on the first row are exactly 'A' to 'Z' and the disc can be rolled. The specific rules of disc rotation will be explained separately below. When the $i$th disc receives a signal(location $j$ for example) from the $(i-1)$th disc(the signal to disc 1 is from the first part), it finds the letter at position $j$ on the first row of itself, then it finds the position of the same letter on the second row and issues a signal to the $(i+1)$th disc. The signal of the $n$th disc is sent to the third part.
For example, at first, the first row of a disc is "ABCDEFGHIJKLMNOPQRSTUVWXYZ" and the second row is "ZYXWVUTSRQPONMLKJIHGFEDCBA". If we roll the disc one time, the first row will become "BCDEFGHIJKLMNOPQRSTUVWXYZA" and the second row will become "YXWVUTSRQPONMLKJIHGFEDCBAZ". If the disc receives a signal 'C'(3) , because the third letter on the first row now is 'D', which is at the $22$nd position of the second row. The disc should issue a signal 22 to the next disc.
The third part, ]reflector, works as a function $f$ from $\{A,B,...,Z\}$ to $\{A,B,...,Z\}$ where $f(x)\not= x$ and $f(f(x))=x$. When the reflector receives a signal(location $5$, letter 'E' for example) from the $n$th disc of the second part, it issues a signal of $f(E)$ back to the $n$th disc.
Then signals will be sent back to the $1$st disc as it does from the $1$st disc to the $n$th disc. The only difference is that this time each disc finds the letter at position $j$ on the second row of itself and finds the position of the same letter on the first row.
Each time a key on the keyboard is pressed, the first disc rolls one time immediately (before any signal flow). Once the $i$th ($1\leq i\leq n-1$) disc is rolled $T$ times ($T\geq 1,T\pmod {26}=0$), the $(i+1)$th disc will be rolled once. The rotation of the n-th disc has no effect.
Lucida and Kanari roll some discs at first and start to transmit the message. Now Lucida has sent $Q$ messages to Kanari, please help Kanari to decipher these messages.
You can refer to the diagram below to better understand the usage of this Enigma. It shows the decryption process of the first three letters in the first sample.
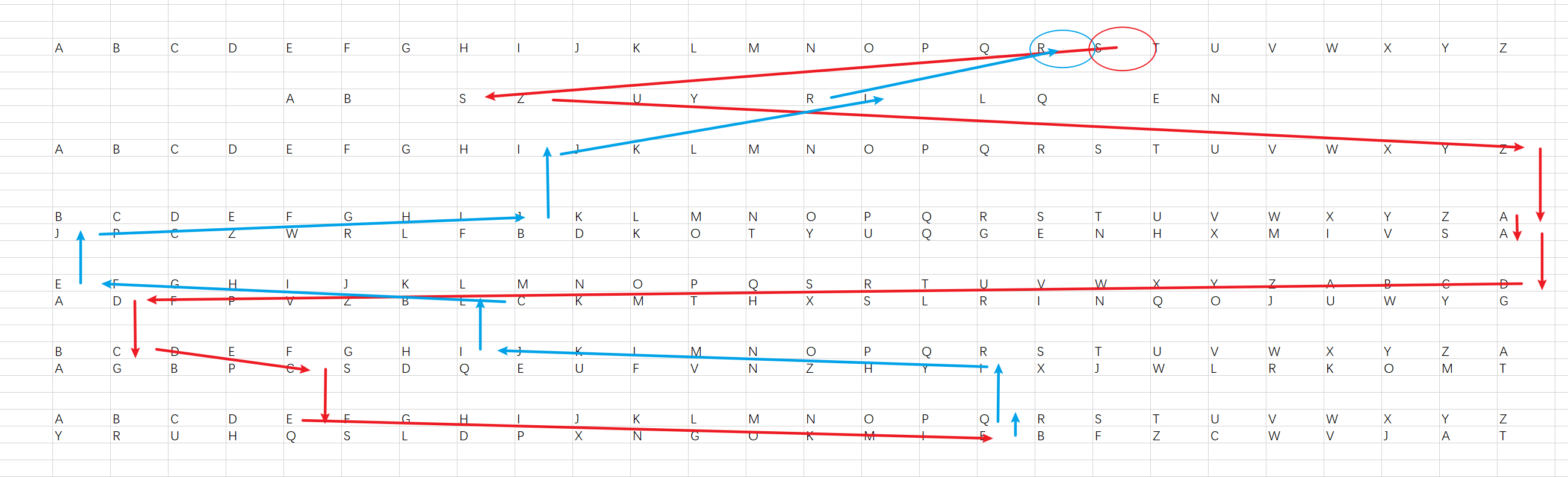
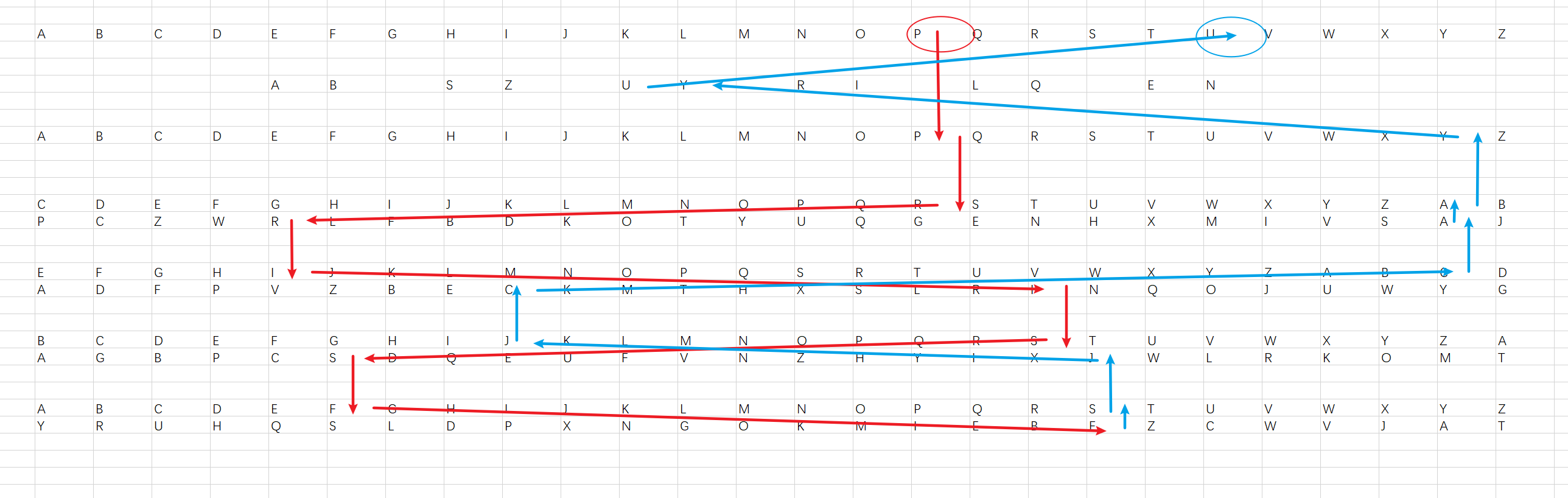
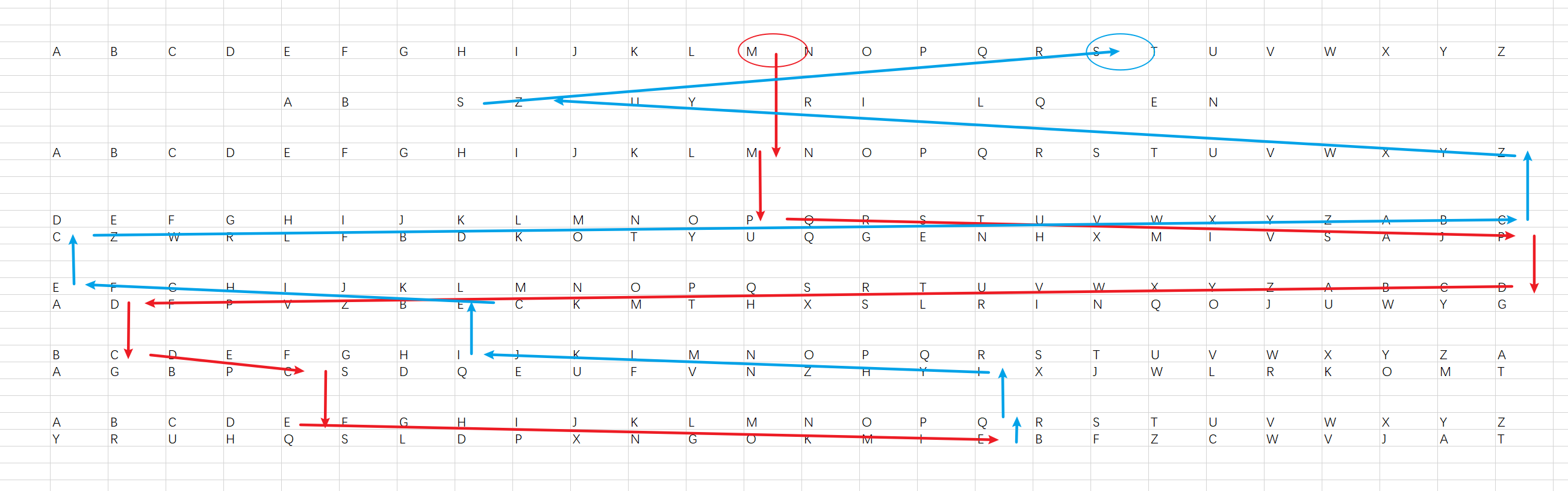
Lucida and Kanari were playing Counter-Strike: Global Offensive and needed frequent tactical exchanges. Losing interphone, they had to do radio communication, but the ease with which transmissions could be intercepted meant strong encryption became vital. They chose to adopt inventor Arthur Scherbius's Enigma machine, which was used by the German army during World War 2 and offered an unprecedented level of encryption.
When a letter key is pressed on the Enigma keyboard an electrical signal flows into a scrambler disc. This disc has 26 inputs and 26 outputs which are connected internally in a random fashion, so a signal entering at input $1$ may exit at output $14$. The signal passes through $n$ of these discs then is reflected so it passes back through the same $n$ discs again, before finally displaying the enciphered letter on a lampboard.
So far this is just a monoalphabetic substitution cipher, however, Enigma's strength comes from the fact that the discs rotate. The first disc rotates on every press, when it rotates a whole circle, it will cause the next disc to rotate and so the second will eventually cause the third disc to rotate and so on. This means the machine is a polyalphabetic cipher that can cycle through $26^n$ unique substitution alphabets before repeating.
To make the machine even more secure, up to 10 pairs of letters on the keyboard can be swapped using patch cables. Combined with the $26^n$ possible starting rotations for the scrambler discs the total number of initial configurations for the machine is large enough to avoid being deciphered.
As long as the machine is set to the correct initial setting it will decipher a message encrypted using the same settings, the initial setting is therefore the key. Lucida and Kanari used a new key for each game and sent out top-secret code books containing the initial Enigma settings every day. The Enigma worked well and they won most of the game by using the secret tactics.
Formally, the Enigma consists of three parts. They are combined with each other via signals. The signals indicate a location between $1$ to $26$, sometimes we may also use 'A' to 'Z' instead of $1$ to $26$ for convenience. When a key on the keyboard is pressed, there will be signals sent from the first part to the second part and then to the third part. After some process, signals will be sent back to the first part and finally become a letter shown on the lampboard.
The first part contains $p$ patch cables that can swap $p$ pairs of letters on the keyboard. It is guaranteed that the 2p letters are distinct. For example, if the letter 'A' and 'B' are swapped, after you pressed 'A', what's actually going into the second part is the signal of 'B'(2); when a signal of 'A'(1) comes from the second part, what's actually shown in front of you is letter 'B'.
The second part are $n$ discs which play the key role of the Enigma. Each disc can be seen as a monoalphabetic substitution cipher. Each disc has two rows up and down, and each row contains an 'A' to 'Z' permutation. Initially, letters on the first row are exactly 'A' to 'Z' and the disc can be rolled. The specific rules of disc rotation will be explained separately below. When the $i$th disc receives a signal(location $j$ for example) from the $(i-1)$th disc(the signal to disc 1 is from the first part), it finds the letter at position $j$ on the first row of itself, then it finds the position of the same letter on the second row and issues a signal to the $(i+1)$th disc. The signal of the $n$th disc is sent to the third part.
For example, at first, the first row of a disc is "ABCDEFGHIJKLMNOPQRSTUVWXYZ" and the second row is "ZYXWVUTSRQPONMLKJIHGFEDCBA". If we roll the disc one time, the first row will become "BCDEFGHIJKLMNOPQRSTUVWXYZA" and the second row will become "YXWVUTSRQPONMLKJIHGFEDCBAZ". If the disc receives a signal 'C'(3) , because the third letter on the first row now is 'D', which is at the $22$nd position of the second row. The disc should issue a signal 22 to the next disc.
The third part, ]reflector, works as a function $f$ from $\{A,B,...,Z\}$ to $\{A,B,...,Z\}$ where $f(x)\not= x$ and $f(f(x))=x$. When the reflector receives a signal(location $5$, letter 'E' for example) from the $n$th disc of the second part, it issues a signal of $f(E)$ back to the $n$th disc.
Then signals will be sent back to the $1$st disc as it does from the $1$st disc to the $n$th disc. The only difference is that this time each disc finds the letter at position $j$ on the second row of itself and finds the position of the same letter on the first row.
Each time a key on the keyboard is pressed, the first disc rolls one time immediately (before any signal flow). Once the $i$th ($1\leq i\leq n-1$) disc is rolled $T$ times ($T\geq 1,T\pmod {26}=0$), the $(i+1)$th disc will be rolled once. The rotation of the n-th disc has no effect.
Lucida and Kanari roll some discs at first and start to transmit the message. Now Lucida has sent $Q$ messages to Kanari, please help Kanari to decipher these messages.
You can refer to the diagram below to better understand the usage of this Enigma. It shows the decryption process of the first three letters in the first sample.



输入解释
This problem contains multiple test cases.
The first line contains a single integer $T$($1\leq T\leq 25$).
Then $T$ test cases follow.
For each test case, on the first line is an integer $p$, the number of patch cables.($1\leq p\leq 10$).
The next following $p$ lines describe these patch cables. Each line contains two characters separated by no spaces, which means they are swapped by the patch cables.
Then an integer $D$ on the next line, the number of discs. ($1\leq D\leq 50$)
The next following $D$ lines describe these discs. Each line contains a string of length 26. The string of the $i$th line is the second row of the $i$th disc initially. (The first row is "ABCDEFGHIJKLMNOPQRSTUVWXYZ" initially)
The next line contains D space-separated integers $d_i$, Lucida and Kanari roll the $i$th disc $d_i$ times before they transmit. ($0 \leq d_i\leq 25$).
The next line is a string $r$ of length 26, which describes the reflector. $f(A)=r_1, f(B)=r_2, ... , f(Z)=r_{26}$.
Then an integer $Q$ on the next line, the number of messages Lucida sends to Kanari. ($1\leq Q\leq 10$, and the length of each message is less than 50).
In the last $Q$ lines, each line contains a message Lucida sends.
The first line contains a single integer $T$($1\leq T\leq 25$).
Then $T$ test cases follow.
For each test case, on the first line is an integer $p$, the number of patch cables.($1\leq p\leq 10$).
The next following $p$ lines describe these patch cables. Each line contains two characters separated by no spaces, which means they are swapped by the patch cables.
Then an integer $D$ on the next line, the number of discs. ($1\leq D\leq 50$)
The next following $D$ lines describe these discs. Each line contains a string of length 26. The string of the $i$th line is the second row of the $i$th disc initially. (The first row is "ABCDEFGHIJKLMNOPQRSTUVWXYZ" initially)
The next line contains D space-separated integers $d_i$, Lucida and Kanari roll the $i$th disc $d_i$ times before they transmit. ($0 \leq d_i\leq 25$).
The next line is a string $r$ of length 26, which describes the reflector. $f(A)=r_1, f(B)=r_2, ... , f(Z)=r_{26}$.
Then an integer $Q$ on the next line, the number of messages Lucida sends to Kanari. ($1\leq Q\leq 10$, and the length of each message is less than 50).
In the last $Q$ lines, each line contains a message Lucida sends.
输出解释
For each message Lucida sends to Kanari, decipher it and output it in a single line. You need to output $\sum Q$ lines in total.
输入样例
3 6 AB SZ UY RI TO EN 3 AJPCZWRLFBDKOTYUQGENHXMIVS UWYGADFPVZBECKMTHXSLRINQOJ TAGBPCSDQEUFVNZHYIXJWLRKOM 0 4 1 YRUHQSLDPXNGOKMIEBFZCWVJAT 1 SPMFK 3 YE KV XA 1 LEPNXCURDYZWIQFKHGVSBAMJOT 2 WMVRLXOQTKJEBZGYHDUISCAFPN 5 O J B K ULQJMBQOM 3 JA BQ SG 2 MNZBFLVCGWTQOKEPYXSARHIJDU WXIFKOEVMQLZNUBDCSAPTRHGJY 24 2 KNEICYZODRATUBHQPJWLMXSVFG 9 THE QUCIK BROWN FOX JUMPS OVER A LAZT DOG
输出样例
RUSHB C C P C NORTHEAST QEM ZJVBU CPUUG QWK DAHJR WBKO V GVEC KJR
来自杭电HDUOJ的附加信息
| Hint | Though Lucida and Kanari didn't roll the first disc before they start, it was rolled for the first time as the moment Lucida pressed the first letter.After a message was sent, Lucida and Kanari would not roll the discs back to their initial states.In the third sample, when the second letter 'H' is pressed, the first disc has already been rolled 26 times so it causes the second disc to roll.In fact, when you input the plaintext, you will get the ciphertext. When you input the ciphertext into the cipher machine of the same state, you will also get the plaintext the same as your input before. |
最后修改于 2021-10-23T19:11:32+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 262144/262144K(Java/Others) |
登陆或注册以提交代码