当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
7046:Fall with Trees
题目描述
Fall wants to draw a perfect binary tree.
We first stipulate that all nodes in the tree with the same depth also have the same y-coordinate in the plane. Define nodes with the same depth to be nodes at the same level, then the perfect binary tree has four properties.
- It is a full binary tree.
- The difference between the y-coordinates of two nodes at each adjacent level is a constant.
- The difference between the x-coordinates of two adjacent nodes at the same level is constant.
- The x-coordinate of each node is the average of the x-coordinates of its sons.
Fall has drawn the root node and its left and right sons of this binary tree. Now Fall intends to draw a total of $k$ levels and cut the binary tree down and paste it on the wall afterwards, so he wants to know what is the area of the convex hull of all nodes of this perfect binary tree.
Here's the picture of the perfect binary tree for the first example, whose area is $S_{ABC}+S_{BCGD}=14$
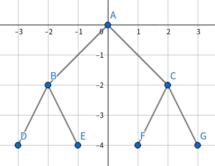
We first stipulate that all nodes in the tree with the same depth also have the same y-coordinate in the plane. Define nodes with the same depth to be nodes at the same level, then the perfect binary tree has four properties.
- It is a full binary tree.
- The difference between the y-coordinates of two nodes at each adjacent level is a constant.
- The difference between the x-coordinates of two adjacent nodes at the same level is constant.
- The x-coordinate of each node is the average of the x-coordinates of its sons.
Fall has drawn the root node and its left and right sons of this binary tree. Now Fall intends to draw a total of $k$ levels and cut the binary tree down and paste it on the wall afterwards, so he wants to know what is the area of the convex hull of all nodes of this perfect binary tree.
Hint
Here's the picture of the perfect binary tree for the first example, whose area is $S_{ABC}+S_{BCGD}=14$

输入解释
The input consists of multiple test cases.
The first line contains an integer $T$ ($T \leq 2\times 10^5$) -- the number of test cases.
For each test case:
In the first line, there is an integer $k$ ($2 \leq k \leq 10^4$).
In the second line, there are six integers $x_{root},y_{root},x_{lson},y_{lson},x_{rson},y_{rson}\in [-10^4,10^4]$ ,which represent the coordinates of the root node and its sons.
It is guaranteed that all the coordinates meet the conditions of the question, which means:
- $x_{lson}+x_{rson}=2\times x_{root}$
- $y_{lson}=y_{rson}$
- $y_{root}>y_{lson},x_{lson}<x_{rson}$
The first line contains an integer $T$ ($T \leq 2\times 10^5$) -- the number of test cases.
For each test case:
In the first line, there is an integer $k$ ($2 \leq k \leq 10^4$).
In the second line, there are six integers $x_{root},y_{root},x_{lson},y_{lson},x_{rson},y_{rson}\in [-10^4,10^4]$ ,which represent the coordinates of the root node and its sons.
It is guaranteed that all the coordinates meet the conditions of the question, which means:
- $x_{lson}+x_{rson}=2\times x_{root}$
- $y_{lson}=y_{rson}$
- $y_{root}>y_{lson},x_{lson}<x_{rson}$
输出解释
For each test case, output a real number representing the answer, with three decimal places.
输入样例
3 3 0 0 -2 -2 2 -2 4 0 0 -4 -2 4 -2 10000 0 0 -10000 -10000 10000 -10000
输出样例
14.000 54.000 3999000000000.000
最后修改于 2021-10-23T19:11:11+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 524288/524288K(Java/Others) |
登陆或注册以提交代码