当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
6904:Death by Thousand Cuts
题目描述
While Jonathan was doing his math homework, he found a multiple-choice question:
Given a cuboid with each edge parallel to the coordinate axis, two vertexes of which are (0,0,0) and (a,b,c), and a plane Ax + By + Cz + D = 0 which intersects the cuboid. You are asked to calculate the number of edges of the cross section. Four options are provided: A. three, B. four, C. five and D. six.
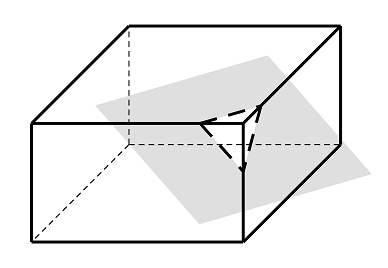
Unfortunately, the number D has been covered by black ink so Jonathan didn’t know what exactly it is. Therefore, D couldbe the anyreal number satisfyingthe plane intersectsthe cuboid in equal probability.
Then Jonathan found some options had significantly greater probability to be the correct answer in some cases. For example, if the cuboid is (0,0,0),(1,1,1) and the plane is x+y+D = 0, then the option B has the 100% probability to be the right answer. Therefore, he wanted to know each option’s probability to be the correct answer in normal cases. As the problem is too hard for him, please help him to calculate the answer.
We can prove that the probability of each option is a rational number. Let’s denote it by irreducible fraction Q/P, you are only to print the value Q$\times P^{-1}$ mod $10^9$ + 7. Here $P^{-1}$ is multiplicative inverse of P modulo $10^9$ + 7.
Given a cuboid with each edge parallel to the coordinate axis, two vertexes of which are (0,0,0) and (a,b,c), and a plane Ax + By + Cz + D = 0 which intersects the cuboid. You are asked to calculate the number of edges of the cross section. Four options are provided: A. three, B. four, C. five and D. six.

Unfortunately, the number D has been covered by black ink so Jonathan didn’t know what exactly it is. Therefore, D couldbe the anyreal number satisfyingthe plane intersectsthe cuboid in equal probability.
Then Jonathan found some options had significantly greater probability to be the correct answer in some cases. For example, if the cuboid is (0,0,0),(1,1,1) and the plane is x+y+D = 0, then the option B has the 100% probability to be the right answer. Therefore, he wanted to know each option’s probability to be the correct answer in normal cases. As the problem is too hard for him, please help him to calculate the answer.
We can prove that the probability of each option is a rational number. Let’s denote it by irreducible fraction Q/P, you are only to print the value Q$\times P^{-1}$ mod $10^9$ + 7. Here $P^{-1}$ is multiplicative inverse of P modulo $10^9$ + 7.
输入解释
The first line of the input gives the number of test cases, T (1 ≤ T ≤ $10^4$). T test cases follow.
For each testcase, only one line contains 6 integers a,b,c,A,B,C (1 ≤ a,b,c ≤ $10^4$,0 ≤|A|,|B|,|C|≤ $10^4$, |A|+|B|+|C| > 0), representing the diagonal point (a,b,c) and the parameters of the plane equation.
For each testcase, only one line contains 6 integers a,b,c,A,B,C (1 ≤ a,b,c ≤ $10^4$,0 ≤|A|,|B|,|C|≤ $10^4$, |A|+|B|+|C| > 0), representing the diagonal point (a,b,c) and the parameters of the plane equation.
输出解释
For each test case, print a line with four integers $P_1,P_2,P_3,P_4,$ representing the probability of options A, B, C and D respectively.
输入样例
3 1 2 3 1 1 1 2 2 2 1 1 1 2 2 2 2 -1 1
输出样例
333333336 333333336 333333336 0 666666672 0 0 333333336 500000004 0 500000004 0
来自杭电HDUOJ的附加信息
| Recommend | liuyiding |
最后修改于 2021-06-22T18:18:49+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 262144/262144K(Java/Others) |
登陆或注册以提交代码