当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
6895:PE Class
Special Judge 特殊评判题目描述
This class is on PE. Today, Baby Volcano is going to take part in a running competition in a maze. Could you help him win this competition?
For simplicity, we assume that this maze lies in a Euclidean plane. There is a graphical description for the maze shown in the following figure. We give some explanation here:
1. There are two kinds of obstructions in this maze, walls and doors. In the figure, black segments and rays are walls, red segments are doors. Some doors are closed while others are open. Baby volcano couldn't go through walls and closed doors, while he could pass open doors. He couldn't tell whether a door is open or not before reaching $its\ midpoint$.
2. In the outmost layer there are $5$ pieces of walls, corresponding to segment $GE,EF,FH$, and ray $GI,HJ$.
3. In the inner part there are $n$ layers of obstructions, the obstructions in the $i$-layer lies in $y=i$, consists of $i$ doors and $i-1$ walls, every obstruction is a segment with length $1$. The $j$-th door$(1\leq j \leq i)$ in $i$-th layer is the segement $\left(\left(\frac{1-2i}{2}+2j-2,i\right),\left(\frac{1-2i}{2}+2j-1,i\right)\right)$. The $j$-th wall$(1\leq j \leq i-1)$ in $i$-th layer is the segement
$\left(\left(\frac{1-2i}{2}+2j-1,i\right),\left(\frac{1-2i}{2}+2j,i\right)\right)$
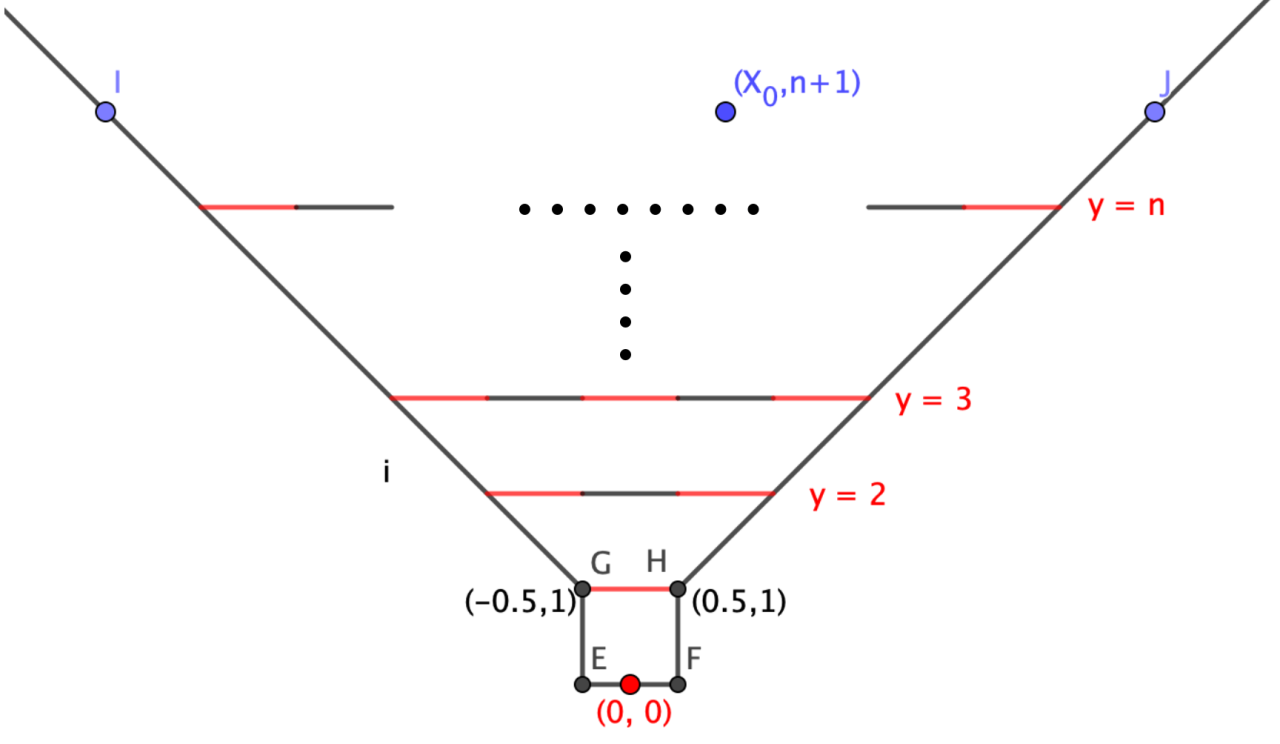
Now for every $1\leq i\leq n$, the teacher uniformly randomly choose $k_i$($1\leq k_i\leq i$) doors to be open. Baby Volcano wonders, if he starts at $(x_0,n+1)$, and try to approach $(0,0)$, what is the minimum expected length of walk?
For simplicity, we assume that this maze lies in a Euclidean plane. There is a graphical description for the maze shown in the following figure. We give some explanation here:
1. There are two kinds of obstructions in this maze, walls and doors. In the figure, black segments and rays are walls, red segments are doors. Some doors are closed while others are open. Baby volcano couldn't go through walls and closed doors, while he could pass open doors. He couldn't tell whether a door is open or not before reaching $its\ midpoint$.
2. In the outmost layer there are $5$ pieces of walls, corresponding to segment $GE,EF,FH$, and ray $GI,HJ$.
3. In the inner part there are $n$ layers of obstructions, the obstructions in the $i$-layer lies in $y=i$, consists of $i$ doors and $i-1$ walls, every obstruction is a segment with length $1$. The $j$-th door$(1\leq j \leq i)$ in $i$-th layer is the segement $\left(\left(\frac{1-2i}{2}+2j-2,i\right),\left(\frac{1-2i}{2}+2j-1,i\right)\right)$. The $j$-th wall$(1\leq j \leq i-1)$ in $i$-th layer is the segement
$\left(\left(\frac{1-2i}{2}+2j-1,i\right),\left(\frac{1-2i}{2}+2j,i\right)\right)$

Now for every $1\leq i\leq n$, the teacher uniformly randomly choose $k_i$($1\leq k_i\leq i$) doors to be open. Baby Volcano wonders, if he starts at $(x_0,n+1)$, and try to approach $(0,0)$, what is the minimum expected length of walk?
输入解释
In the first line there is a number $T$, denotes the number of test cases.
Next, there are $2\times T$ lines demonstrating each test case.
For every case, in the first line there are two integers, $n,x_0$, denotes the number of layers in this maze and the start position of Baby Volcano.
In the second line there are $n$ integers $k_1,k_2,k_3,\cdots,k_n$, showing the number of doors open in the $i$-th layer.
The input guarantees that $1 \leq T \leq 100,1 \leq n \leq 50$, and $-n\leq x_0\leq n$.
Next, there are $2\times T$ lines demonstrating each test case.
For every case, in the first line there are two integers, $n,x_0$, denotes the number of layers in this maze and the start position of Baby Volcano.
In the second line there are $n$ integers $k_1,k_2,k_3,\cdots,k_n$, showing the number of doors open in the $i$-th layer.
The input guarantees that $1 \leq T \leq 100,1 \leq n \leq 50$, and $-n\leq x_0\leq n$.
输出解释
Output $T$ real numbers, for each test case, you need to output $d$, denotes the minimum expected length of walk. You need to output six decimal places.
输入样例
4 2 1 1 2 2 1 1 1 3 2 1 2 3 4 2 1 2 2 1
输出样例
3.414213 4.414213 4.828427 10.323520
来自杭电HDUOJ的附加信息
| Recommend | IceyWang |
最后修改于 2020-10-25T23:35:20+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 262144/262144K(Java/Others) |
登陆或注册以提交代码