当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
6883:Coin Game
题目描述
There are $n$ machines in front of you, and each of them has a cute button on it.
For the $i$-th machine, if you push the button on it, it will give you a coin valued at $a_i$. If you push the button again, it will give you a coin valued at $b_i$. If you push the button the third time, it will give you a coin valued at $a_i$ again. However, it won't give you coins any more even you push the button because the $i$-th machine only has three coins.
Now you want to obtain $k$ coins from these machines, and you should make the total value of these coins as maximum as possible. Let's denote the maximum total value of these $k$ coins as $f(k)$.
You are required to output the value of $f(1) \oplus f(2) \oplus f(3) \oplus \cdots \oplus f(m)$, where $m$ is a given number and $\oplus$ means the xor operatation.
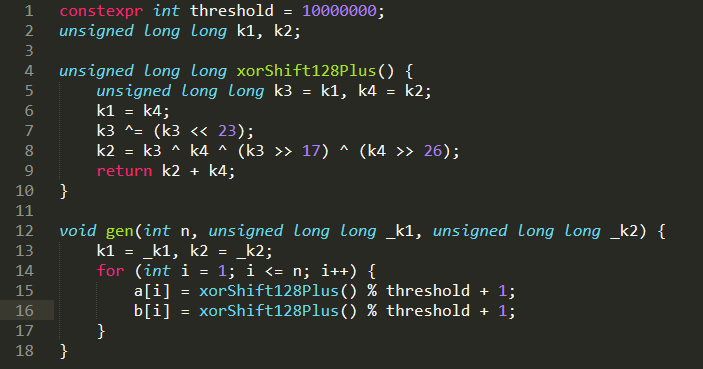
To avoid spending too much time reading all the data, we use xorshift128plus algorithm to generate the testdata, this algorithm is parameterized with two initial seed $k_1$ and $k_2$. Please refer to the code (written in C++) in the below:
In the first test case of the sample input, there are $2$ machines, and the first machine will give you the coins valued at $(406905, 1803337, 406905)$ and $(491922, 4734236, 491922)$.
$f(1) = 491922, f(2) = 5226158, f(3) = 5718080, f(4) = 7436400, f(5) = 7928322, f(6) = 8335227$
For the $i$-th machine, if you push the button on it, it will give you a coin valued at $a_i$. If you push the button again, it will give you a coin valued at $b_i$. If you push the button the third time, it will give you a coin valued at $a_i$ again. However, it won't give you coins any more even you push the button because the $i$-th machine only has three coins.
Now you want to obtain $k$ coins from these machines, and you should make the total value of these coins as maximum as possible. Let's denote the maximum total value of these $k$ coins as $f(k)$.
You are required to output the value of $f(1) \oplus f(2) \oplus f(3) \oplus \cdots \oplus f(m)$, where $m$ is a given number and $\oplus$ means the xor operatation.
To avoid spending too much time reading all the data, we use xorshift128plus algorithm to generate the testdata, this algorithm is parameterized with two initial seed $k_1$ and $k_2$. Please refer to the code (written in C++) in the below:

Hint
In the first test case of the sample input, there are $2$ machines, and the first machine will give you the coins valued at $(406905, 1803337, 406905)$ and $(491922, 4734236, 491922)$.
$f(1) = 491922, f(2) = 5226158, f(3) = 5718080, f(4) = 7436400, f(5) = 7928322, f(6) = 8335227$
输入解释
There are multiple test cases,please read until the end of the file.
For each test case, it contains only four integer $n, m, k_1, k_2$. $1 \le n \le 5\times 10^6$, $1 \le m \le 1.5 \times 10^7$, $1 \le k_1, k_2 \le 10^{12}$ in one line.
For each test case, it contains only four integer $n, m, k_1, k_2$. $1 \le n \le 5\times 10^6$, $1 \le m \le 1.5 \times 10^7$, $1 \le k_1, k_2 \le 10^{12}$ in one line.
输出解释
Output the answer in one line for each test case.
输入样例
2 6 123456789 987654321 10 20 19260817 71806291
输出样例
6935157 41506271
来自杭电HDUOJ的附加信息
| Recommend | IceyWang |
最后修改于 2020-10-25T23:35:14+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 8000/8000MS(Java/Others) | 262144/262144K(Java/Others) |
登陆或注册以提交代码