当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
6873:Game
题目描述
There are $n$ columns of blocks standing in a row. The $i$-th column has $a_i$ blocks in the beginning. Each block has size $1\times 1\times 1$. Define $(x,y)$ represent the block at column $x$ and is the $y$-th block from bottom to top. You need to support two operations:
- `1 x y` Push one block to the left, that means you choose one block which has no block at its right and make it move to the left. Because of the friction, the block above it will also move to the left, and because the blocks cannot intersect, the block at its left will move to the left either. This will cause a chain reaction. After every block moved, if some blocks hang in the air, then it will fall because of gravitation. Note that the blocks at column $1$ can't move to the left, so if a movement causes a block at column $1$ move, you can't perform this operation.
Formally, let $b_i$ be the number of blocks in the $i$-th column now. If $y> b_x$, you will do nothing. Otherwise, you will choose block $(x,y)$. There are two stages of the movement of blocks. The first stage is moving. Let $l$ be the greatest position that satisfies $1\leq l<x$ and $b_l<y$, then you can perform this operation as long as $l$ exists. Then for all blocks $(i,j)$ that satisfy $l< i\leq x$ and $j\geq y$, it moves to $(i-1,j)$. The second stage is falling. For blocks $(i,j)$ ($j>1$) that there are no blocks in $(i,j-1)$, it falls to $(i,j-1)$. Repeat doing it until no blocks satisfy the condition(There is a block in $(i,j)$ and no block in $(i,j-1)$).
Output the number of blocks you have moved in this operation. If $y > b_x$ or you can't perform this problem, the answer is $0$. It's not required that $y > b_{x+1}$ in this problem.
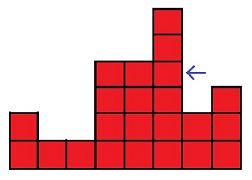
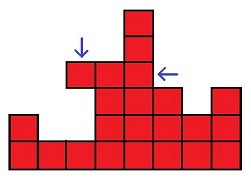

This shows an operation that pushes the block at $(6,4)$, and the value of $l$ is $3$. The number of blocks moved is $5$.
- `2 x` Ask the height of $x$-th column now.
You are also asked to output the height of all columns after all operations.
- `1 x y` Push one block to the left, that means you choose one block which has no block at its right and make it move to the left. Because of the friction, the block above it will also move to the left, and because the blocks cannot intersect, the block at its left will move to the left either. This will cause a chain reaction. After every block moved, if some blocks hang in the air, then it will fall because of gravitation. Note that the blocks at column $1$ can't move to the left, so if a movement causes a block at column $1$ move, you can't perform this operation.
Formally, let $b_i$ be the number of blocks in the $i$-th column now. If $y> b_x$, you will do nothing. Otherwise, you will choose block $(x,y)$. There are two stages of the movement of blocks. The first stage is moving. Let $l$ be the greatest position that satisfies $1\leq l<x$ and $b_l<y$, then you can perform this operation as long as $l$ exists. Then for all blocks $(i,j)$ that satisfy $l< i\leq x$ and $j\geq y$, it moves to $(i-1,j)$. The second stage is falling. For blocks $(i,j)$ ($j>1$) that there are no blocks in $(i,j-1)$, it falls to $(i,j-1)$. Repeat doing it until no blocks satisfy the condition(There is a block in $(i,j)$ and no block in $(i,j-1)$).
Output the number of blocks you have moved in this operation. If $y > b_x$ or you can't perform this problem, the answer is $0$. It's not required that $y > b_{x+1}$ in this problem.



This shows an operation that pushes the block at $(6,4)$, and the value of $l$ is $3$. The number of blocks moved is $5$.
- `2 x` Ask the height of $x$-th column now.
You are also asked to output the height of all columns after all operations.
输入解释
The first line contains an integer $T (1\leq T\leq 5)$ - the number of test cases.
For each test case, the first line contains two integers $n,q (1\leq n, q\leq 2\times 10^5)$. The second line contains $n$ integers $b_1, b_2, \dots, b_n(1\leq b_i\leq 10^9)$. Each of the following $q$ lines contains an operation: `1 x y` ($1\leq x\leq n, 1\leq y \leq 10^9$), or `2 x` $(1\leq x\leq n)$.
For each test case, the first line contains two integers $n,q (1\leq n, q\leq 2\times 10^5)$. The second line contains $n$ integers $b_1, b_2, \dots, b_n(1\leq b_i\leq 10^9)$. Each of the following $q$ lines contains an operation: `1 x y` ($1\leq x\leq n, 1\leq y \leq 10^9$), or `2 x` $(1\leq x\leq n)$.
输出解释
For each test case, output one integer in one line for each operation. Then output $n$ integers in one line - the height of all columns after all operations from left to right in order.
输入样例
1 8 4 2 1 1 4 4 6 2 3 1 6 4 2 5 1 1 1 1 8 2
输出样例
5 6 0 14 2 2 4 6 3 2 3 1
来自杭电HDUOJ的附加信息
| Recommend | IceyWang |
最后修改于 2020-10-25T23:35:07+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 12000/6000MS(Java/Others) | 65536/65536K(Java/Others) |
登陆或注册以提交代码