当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
6862:Hexagon
Special Judge 特殊评判题目描述
It is preferrable to read the pdf statment.
If the world is a hexagon, I will take as many turns as possible before reaching the end.
Cuber QQ has constructed a hexagon grid with radius $n$. This will be better if explained in a picture. For example, this is a hexagon grid with radius $3$:
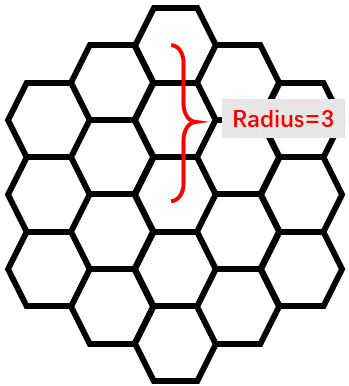
He challenges you take a perfect tour over the hexagon, that is to visit each cell exactly once. Starting from any point in the grid, you can move to any adjacent cell in each step. There are six different directions you can choose from:
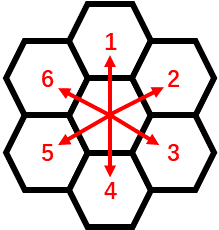
Of course, if you are on the boundary, you cannot move outside of the hexagon.
Let $D(x,y)$ denote the direction from cell $x$ to $y$, and sequence $A$ denotes your route, in which $A_i$ denotes the $i$-th cell you visit. For index $i$ ($1 < i < |A|$), if $D(A_{i-1},A_i) \ne D(A_i,A_{i+1})$, we say there is a turning on cell $i$.
Maximize the number of turning while ensuring that each cell is visited exactly once. Print your route. If there are multiple solution, print any.
If the world is a hexagon, I will take as many turns as possible before reaching the end.
Cuber QQ has constructed a hexagon grid with radius $n$. This will be better if explained in a picture. For example, this is a hexagon grid with radius $3$:

He challenges you take a perfect tour over the hexagon, that is to visit each cell exactly once. Starting from any point in the grid, you can move to any adjacent cell in each step. There are six different directions you can choose from:

Of course, if you are on the boundary, you cannot move outside of the hexagon.
Let $D(x,y)$ denote the direction from cell $x$ to $y$, and sequence $A$ denotes your route, in which $A_i$ denotes the $i$-th cell you visit. For index $i$ ($1 < i < |A|$), if $D(A_{i-1},A_i) \ne D(A_i,A_{i+1})$, we say there is a turning on cell $i$.
Maximize the number of turning while ensuring that each cell is visited exactly once. Print your route. If there are multiple solution, print any.
输入解释
The first line of the input contains a single integer $T$ ($1\le T\le 10^4$), denoting the number of test cases.
Each of the next $T$ cases:
The first line contains an integer $n$ ($2\le n\le 500$).
It is guaranteed that the sum of $n$ doesn't exceed $2 \cdot 10^4$.
Each of the next $T$ cases:
The first line contains an integer $n$ ($2\le n\le 500$).
It is guaranteed that the sum of $n$ doesn't exceed $2 \cdot 10^4$.
输出解释
For each test case, output one line contains a string with $3(n-1)n$ characters. The $i$-th character is $D(A_i,A_{i+1})$.
输入样例
1 2
输出样例
313456
来自杭电HDUOJ的附加信息
| Recommend | IceyWang |
最后修改于 2020-10-25T23:35:01+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/2000MS(Java/Others) | 524288/524288K(Java/Others) |
登陆或注册以提交代码