当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
6816:Boring Game
题目描述
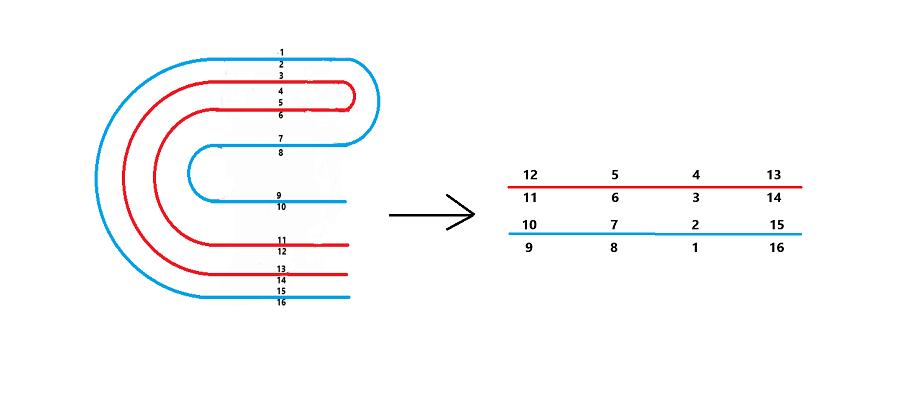
Given $n$ sheets of paper, place them on the table in pile and fold them in half $k$ times from left to right.
Now from top to bottom, mark a number on paper at each side of the front and back. So there are $2 \times n \times 2^k$ numbers in total and these numbers form a permutation $P$.
Now it expands to its original. These numbers from top to bottom, from front to back, from left to right form a permutation $Q$.
Given the permutation $P$, find the permutation $Q$.
See example for details.
For $k=1$ and $P=1..4 \times n$, you can assume that you are marking the page numbers before printing a booklet forming from $n$ pieces of $A4$ papers.
Now from top to bottom, mark a number on paper at each side of the front and back. So there are $2 \times n \times 2^k$ numbers in total and these numbers form a permutation $P$.
Now it expands to its original. These numbers from top to bottom, from front to back, from left to right form a permutation $Q$.
Given the permutation $P$, find the permutation $Q$.
See example for details.
For $k=1$ and $P=1..4 \times n$, you can assume that you are marking the page numbers before printing a booklet forming from $n$ pieces of $A4$ papers.
输入解释
The first line contains a single integer $T(1 \leq T \leq 30)$ , the number of test cases.
For each test case, the first line gives two integers $n$, $k$($1 \leq n \leq 200, 1 \leq k \leq 10$).
The next line gives the permutation $P$ that consists of $2 \times n \times 2^k$ integers $p_i(1 \leq p_i \leq 2 \times n \times 2^k)$.
It is guaranteed that $ \sum 2 \times n \times 2^k$ doesn't exceed $10^6$.
For each test case, the first line gives two integers $n$, $k$($1 \leq n \leq 200, 1 \leq k \leq 10$).
The next line gives the permutation $P$ that consists of $2 \times n \times 2^k$ integers $p_i(1 \leq p_i \leq 2 \times n \times 2^k)$.
It is guaranteed that $ \sum 2 \times n \times 2^k$ doesn't exceed $10^6$.
输出解释
The output should contain $T$ lines each containing $2 \times n \times 2^k$ integers separated by spaces, indicating the permutation $Q$.
输入样例
1 2 2 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
输出样例
12 5 4 13 11 6 3 14 10 7 2 15 9 8 1 16 [hint][\hint]
来自杭电HDUOJ的附加信息
| Recommend | IceyWang |
最后修改于 2020-10-25T23:34:38+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 131072/131072K(Java/Others) |
登陆或注册以提交代码