当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
6814:Tetrahedron
题目描述
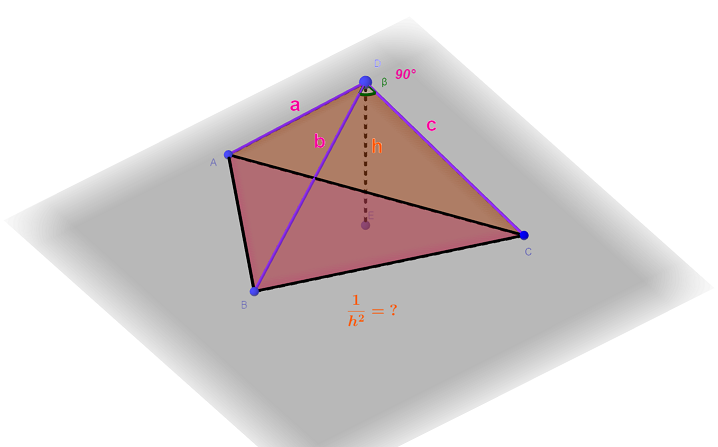
Generate three integers $a$, $b$, and $c$ in $[1,n]$ with equal probability independently, and use them as the three right-angle side length of a right-angled tetrahedron. Find the expectation of the reciprocal square of the distance from the right-angle apex to the slope (Euclidean distance).
For each test case, output a line containing the answer mod $998244353$.
For each test case, output a line containing the answer mod $998244353$.

输入解释
In the first line, you should read an integer $T$ denoting the number of test cases.
In every test case, the only line will include an integer $n$.
It is guaranteed that $T$ is no larger than $2 \times 10^6$ and $n$ is no larger than $6 \times 10^6$.
In every test case, the only line will include an integer $n$.
It is guaranteed that $T$ is no larger than $2 \times 10^6$ and $n$ is no larger than $6 \times 10^6$.
输出解释
For each test case, output the only line containing just one integer denoting the answer mod $998244353$.
输入样例
3 1 2 3
输出样例
3 124780546 194103070
来自杭电HDUOJ的附加信息
| Recommend | IceyWang |
最后修改于 2020-10-25T23:34:37+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 9000/4500MS(Java/Others) | 524288/524288K(Java/Others) |
登陆或注册以提交代码