当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
6798:Triangle Collision
Special Judge 特殊评判题目描述
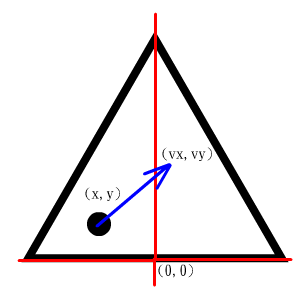
As depicted in the picture above, there is an extremely small ball inside the area enclosed by an equilateral triangular border whose side length is $L$. The radius of the ball is $10^{-1000}$, which is so small that the ball can be treated as a point.
In order to clearly describe the position of the ball, we build a plane coordinate system based on this triangle. The original point is at the midpoint of the triangle's bottom edge, the X-axis is along with the bottom edge (from left to right), and the Y-axis is along with the height on the bottom edge (from bottom to top). For example, the vertices of the triangle are at the positions $\left(-\frac{L}{2}, 0\right)$, $\left(0, \frac{\sqrt{3} L}{2}\right)$ and $\left(\frac{L}{2}, 0\right)$ respectively.
At the beginning, the speed of the ball in the horizontal direction is $v_x$ per second, and that in the vertical direction is $v_y$ per second, in other words, the original speed of the ball is $\sqrt{{v_x}^2 + {v_y}^2}$, along with the direction vector $(v_x, v_y)$.
If the ball is now at the position $(x, y)$, then it will move to the position $(x + t \cdot v_x, y + t \cdot v_y)$ after $t$ seconds, if it does not touch the border during this process.
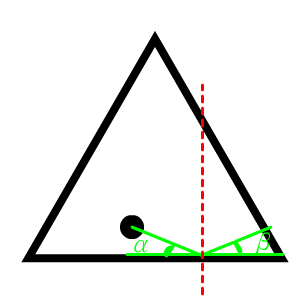
When the ball hits any edge of the border, a completely elastic collision occurs, which means the moving direction of this ball will change according to the law of reflection, but its speed will not.
The law of reflection follows the rule of "incident angle equals reflection angle". As depicted in the picture above, the incident angle $\alpha$ is equal to the reflection angle $\beta$.
Now given the side length $L$ of this triangle, the ball's position $(x, y)$ and its speed $(v_x, v_y)$ at the beginning, can you calculate the time when the $k$-th collision occurs?
It is guaranteed that the ball does not touch any vertex of the triangle within the first $k$ collisions.
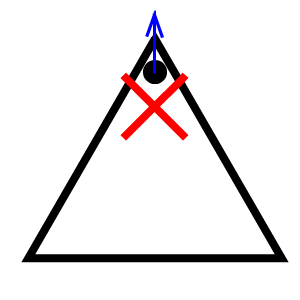
But after the first $k$ collisions, the ball may touch any vertex of the triangle, for example, in the third sample case.
The claim that the ball does not touch any vertex of the triangle means that the distances from the ball to the nearest two sides of the triangle will not equal to the ball's radius at the same time.
输入解释
There are several test cases.
The first line contains an integer $T$ $(1 \leq T \leq 10^4)$, denoting the number of test cases. Then follow all the test cases.
For each test case, the only line contains six integers $L$, $x$, $y$, $v_x$, $v_y$ and $k$ $(1 \leq L \leq 10^4, -10^4 \leq x, y, v_x, v_y \leq 10^4, 1 \leq k \leq 10^6)$, representing a problem.
It is guaranteed for all test cases that the ball is strictly inside the triangle at the beginning, and as mentioned above, does not touch any vertex of the triangle within the first $k$ collisions.
It is also guaranteed for all test cases that the speed of the ball is greater than $0$.
The first line contains an integer $T$ $(1 \leq T \leq 10^4)$, denoting the number of test cases. Then follow all the test cases.
For each test case, the only line contains six integers $L$, $x$, $y$, $v_x$, $v_y$ and $k$ $(1 \leq L \leq 10^4, -10^4 \leq x, y, v_x, v_y \leq 10^4, 1 \leq k \leq 10^6)$, representing a problem.
It is guaranteed for all test cases that the ball is strictly inside the triangle at the beginning, and as mentioned above, does not touch any vertex of the triangle within the first $k$ collisions.
It is also guaranteed for all test cases that the speed of the ball is greater than $0$.
输出解释
For each case, output in one line a real number, denoting the time when the $k$-th collision occurs.
For each output value, your answer is considered correct if its absolute or relative error does not exceed $10^{-4}$. Formally, let your answer be $a$ and the jury's answer be $b$, and then your answer is considered correct if $\frac{|a - b|}{\max(1, |b|)} \leq 10^{-4}$.
For each output value, your answer is considered correct if its absolute or relative error does not exceed $10^{-4}$. Formally, let your answer be $a$ and the jury's answer be $b$, and then your answer is considered correct if $\frac{|a - b|}{\max(1, |b|)} \leq 10^{-4}$.
输入样例
4 4000 0 1732 1000 0 1 4000 0 1732 1000 0 1000000 4000 0 1234 0 -1 1 4000 -1000 1 0 1000 925469
输出样例
1.00002957 1999998.99997035 1233.99999975 1602959.32782988
来自杭电HDUOJ的附加信息
| Recommend | liuyiding |
最后修改于 2020-10-25T23:34:27+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/2000MS(Java/Others) | 524288/524288K(Java/Others) |
登陆或注册以提交代码