当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
6753:Cookies
题目描述
Elsa’s elder brother Eric has got n cookies in his icebox and each cookie has a special number written on it. Let’s denote the number written on the $i^{th}$ cookie by $f_i$. $f_i$ is defined as follows:
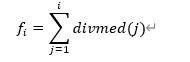
Here, divmed(x) states the median value of divisors of x. Let x has k divisors, then divmed(x) is $\lceil{k/2}\rceil^{th}$ smallest divisor. For example, divmed(100)=10, divmed(10)=2, divmed(1)=1.
One day, Eric opened the icebox and recognized that some of his cookies are missing. His sister Elsa had eaten some of them.
On the first day, she ate cookies that have multiples of $p_1$ as indexes and then, re-indexed them starting from 1 according to their original order. In the same way, she ate cookies with multiples of $p_i$ as indexes on the $i^{th}$ day and re-indexed them. If there were less than $p_i$ cookies left, she ate none of them. Elsa continued to do so for m days.
As Elsa is keen on math and Eric didn’t want to blame his sister, Eric asked her to find out the number written on the $k^{th}$ of remaining cookies.
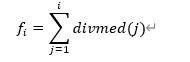
Here, divmed(x) states the median value of divisors of x. Let x has k divisors, then divmed(x) is $\lceil{k/2}\rceil^{th}$ smallest divisor. For example, divmed(100)=10, divmed(10)=2, divmed(1)=1.
One day, Eric opened the icebox and recognized that some of his cookies are missing. His sister Elsa had eaten some of them.
On the first day, she ate cookies that have multiples of $p_1$ as indexes and then, re-indexed them starting from 1 according to their original order. In the same way, she ate cookies with multiples of $p_i$ as indexes on the $i^{th}$ day and re-indexed them. If there were less than $p_i$ cookies left, she ate none of them. Elsa continued to do so for m days.
As Elsa is keen on math and Eric didn’t want to blame his sister, Eric asked her to find out the number written on the $k^{th}$ of remaining cookies.
输入解释
The first line of the input contains an integer T(1≤T≤60), denoting the number of test cases. The first line of each test case contains 3 positive integers n(1≤n≤$10^{10}$), m(1≤m≤$10^5$) and k(1≤k≤$10^{10}$). The next line contains m integers $p_1$,$p_2$,$ \cdots $,$p_m$ (1≤$p_i$≤$10^{10}$).
输出解释
For each test case, output one line containing the answer. If the $k^{th}$ cookie doesn’t exist, then output -1 in a single line.
输入样例
2 25 5 9 3 5 8 12 10 25 5 2 3 5 8 12 10
输出样例
31 2
来自杭电HDUOJ的附加信息
| Recommend | liuyiding |
最后修改于 2020-10-25T23:34:04+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 9000/4500MS(Java/Others) | 524288/524288K(Java/Others) |
登陆或注册以提交代码