当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
6692:Line Graphs
题目描述
Last year, Rounddog participated in a contest with a pretty hard problem set and failed in solving the problem about line graphs. So he decides to make a deep study of line graphs these days.
In the mathematical discipline of graph theory, the line graph of a simple undirected graph $G$ is another simple undirected graph $L(G)$ that represents the adjacency between every two edges in $G$.
Precisely speaking, for an undirected graph $G$ without loops or multiple edges, its line graph $L(G)$ is a graph such that
- each vertex of $L(G)$ represents an edge of $G$; and
- two vertices of $L(G)$ are adjacent if and only if their corresponding edges share a common endpoint in $G$.
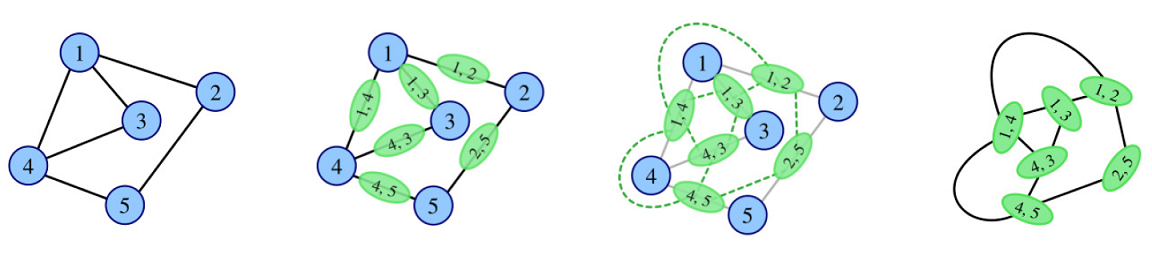
Given a simple undirected graph $G$, Rounddog's study aims to find the maximum cliques in its line graph $L(G)$ and he decides to make some critical results of his early study as a challenge for you.
In this problem, you are given a simple undirected graph $G$ and a small positive integer $k$. After finding all maximum cliques in $L^k(G)$, where $L^0(G)=G$ and $L^s(G)=L(L^{s-1}(G))$ for each positive integer $s$, you need to show Rounddog the number of vertices in one of the maximum cliques and the number of distinct maximum cliques modulo $1\,000\,000\,007$.
Here a subset of vertices of an undirected graph is called clique if and only if there is an edge between each pair of vertices in the subset, and maximum cliques are those cliques with the maximum number of vertices.
In the mathematical discipline of graph theory, the line graph of a simple undirected graph $G$ is another simple undirected graph $L(G)$ that represents the adjacency between every two edges in $G$.
Precisely speaking, for an undirected graph $G$ without loops or multiple edges, its line graph $L(G)$ is a graph such that
- each vertex of $L(G)$ represents an edge of $G$; and
- two vertices of $L(G)$ are adjacent if and only if their corresponding edges share a common endpoint in $G$.

Given a simple undirected graph $G$, Rounddog's study aims to find the maximum cliques in its line graph $L(G)$ and he decides to make some critical results of his early study as a challenge for you.
In this problem, you are given a simple undirected graph $G$ and a small positive integer $k$. After finding all maximum cliques in $L^k(G)$, where $L^0(G)=G$ and $L^s(G)=L(L^{s-1}(G))$ for each positive integer $s$, you need to show Rounddog the number of vertices in one of the maximum cliques and the number of distinct maximum cliques modulo $1\,000\,000\,007$.
Here a subset of vertices of an undirected graph is called clique if and only if there is an edge between each pair of vertices in the subset, and maximum cliques are those cliques with the maximum number of vertices.
输入解释
The input contains several test cases, and the first line contains a single integer $T~(1 \le T \le 1\,000)$, the number of test cases.
For each test case, the first line contains three integers $n~(1 \le n \le 100\,000)$, $m~(0 \le m \le 200\,000)$ and $k~(1 \le k \le 4)$, the number of vertices and edges in the given simple undirected graph $G$ and the number of iterations of the line graph operation.
Then $m$ lines follow, describing all edges of the graph.
Each line of them contains two integers $u$ and $v~(1 \le u, v \le n, u \ne v)$, representing an edge between the $u$-th vertex and the $v$-th vertex.
It is guaranteed that the sum of $n$ in all test cases does not exceed $2\,000\,000$, the sum of $m$ does not exceed $3\,000\,000$, and the graph in each test case contains no loops or multiple edges.
For each test case, the first line contains three integers $n~(1 \le n \le 100\,000)$, $m~(0 \le m \le 200\,000)$ and $k~(1 \le k \le 4)$, the number of vertices and edges in the given simple undirected graph $G$ and the number of iterations of the line graph operation.
Then $m$ lines follow, describing all edges of the graph.
Each line of them contains two integers $u$ and $v~(1 \le u, v \le n, u \ne v)$, representing an edge between the $u$-th vertex and the $v$-th vertex.
It is guaranteed that the sum of $n$ in all test cases does not exceed $2\,000\,000$, the sum of $m$ does not exceed $3\,000\,000$, and the graph in each test case contains no loops or multiple edges.
输出解释
For each test case, output a single line with two integers, the number of vertices in one of the maximum cliques and the number of distinct maximum cliques modulo $1\,000\,000\,007$.
输入样例
3 5 0 4 5 4 1 1 2 1 3 1 4 1 5 5 4 4 1 2 1 3 1 4 1 5
输出样例
0 1 4 1 6 12
来自杭电HDUOJ的附加信息
| Recommend | chendu |
最后修改于 2020-10-25T23:33:31+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 12000/12000MS(Java/Others) | 524288/524288K(Java/Others) |
登陆或注册以提交代码