当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
6657:Acesrc and Cube Hypernet
题目描述
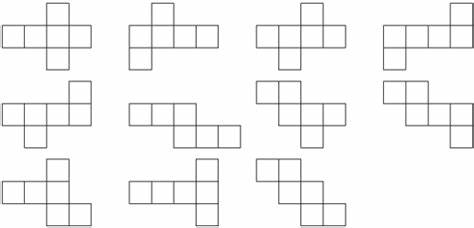
Acesrc is fond of cube nets. If we cut some edges of a cube, the surface of the cube can be unfolded into 2-dimensional space, and the resulting flat shape is called a cube net. There are 11 essentially different cube nets, listed below.
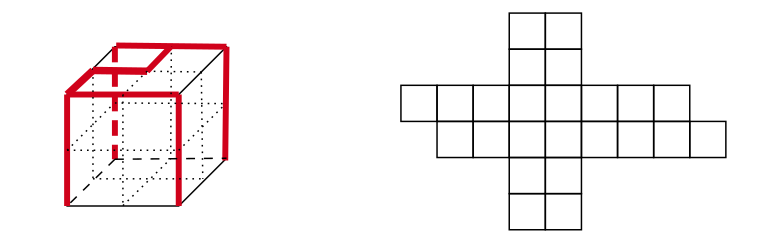
In this problem, we consider a generalization of the cube net, called cube hypernet. For each face of a cube, we divide it into $k \times k$ small square cells. If we cut some edges of these small cells, the surface of the cube can be unfolded into 2-dimensional space, then the resulting flat shape is a cube hypernet. Clearly, cube nets are just a special type of cube hypernets where $k = 1$. The following picture illustrates a cube hypernet and explains how it is formed.
Identifying cube nets is a relatively easy job; however, this might not be true for cube hypernets. Here comes the challenge. Given a flat shape composed of small squares, determine whether it is a cube hypernet.

In this problem, we consider a generalization of the cube net, called cube hypernet. For each face of a cube, we divide it into $k \times k$ small square cells. If we cut some edges of these small cells, the surface of the cube can be unfolded into 2-dimensional space, then the resulting flat shape is a cube hypernet. Clearly, cube nets are just a special type of cube hypernets where $k = 1$. The following picture illustrates a cube hypernet and explains how it is formed.

Identifying cube nets is a relatively easy job; however, this might not be true for cube hypernets. Here comes the challenge. Given a flat shape composed of small squares, determine whether it is a cube hypernet.
输入解释
The first line of the input is a single integer $T$ $(1 \leq T \leq 30)$, denoting the number of test cases.
For each test case, the first line contains two integers $h, w$ $(1 \leq h, w \leq 100)$, denoting the height and width of the input region. Each of the remaining $h$ lines contains $w$ characters, either $\texttt{'#'}$ or $\texttt{'.'}$. The character $\texttt{'#'}$ means that the square is part of the shape, while $\texttt{'.'}$ not.
It is guaranteed that the input shape is nonempty and connected in four directions, and there is no hole inside the shape, not even a hole 8-connected to the outside. Also, the sum of $h \times w$ over all test cases does not exceed 35000.
For each test case, the first line contains two integers $h, w$ $(1 \leq h, w \leq 100)$, denoting the height and width of the input region. Each of the remaining $h$ lines contains $w$ characters, either $\texttt{'#'}$ or $\texttt{'.'}$. The character $\texttt{'#'}$ means that the square is part of the shape, while $\texttt{'.'}$ not.
It is guaranteed that the input shape is nonempty and connected in four directions, and there is no hole inside the shape, not even a hole 8-connected to the outside. Also, the sum of $h \times w$ over all test cases does not exceed 35000.
输出解释
For each test case, output $\texttt{yes}$ in a line if the input shape is cube hypernet, and $\texttt{no}$ otherwise.
输入样例
2 6 9 ...##.... ...##.... ########. .######## ...##.... ...##.... 1 6 ######
输出样例
yes no
来自杭电HDUOJ的附加信息
| Recommend | chendu |
最后修改于 2020-10-25T23:33:14+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/2000MS(Java/Others) | 131072/131072K(Java/Others) |
登陆或注册以提交代码