当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
6360:Kaleidoscope
题目描述
John loves colorful things such as kaleidoscope. When he started to take advantage of Wolfram Alpha, a scientific computing tool, he fell in love with its current logo, a rhombic hexecontahedron, immediately.

Wolfram|Alpha Computational Intelligence$^{\mathrm{TM}}$
The rhombic hexecontahedron is a beautiful polyhedron which has $60$ congruent rhombic faces. A rhombic hexecontahedron can be constructed from a regular dodecahedron, by taking its vertices, its face centers and its edge centers and scaling them in or out from the body center to different extents. Also, a rhombic hexecontahedron can be constructed from a regular icosahedron, by appending three rhombuses to each of its faces such that each rhombus shares a vertex with it and every two rhombuses share an edge.
John wants to make some origami of rhombic hexecontahedron. Before getting started from scratch, he was wondering in how many different ways he can make origami of at most $n$ types of colored paper. He has thought for a while and finally determined to leave this problem for you. Furthermore, he added some restriction such that a way of origami is counted if the number of faces colored by the $i$-th type of paper is at least $c_i$ $(i = 1, 2, \cdots, n)$. Of course, the answer might be so large, so you just need to tell him the answer modulo some integer $p$.
Two ways are considered as the same if and only if there exists a way of rotation that can transform one to another so that each corresponding face has the same color. Here is an example of origami after coloring.
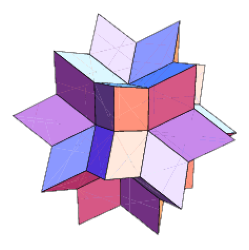
Picture from Wolfram Mathworld
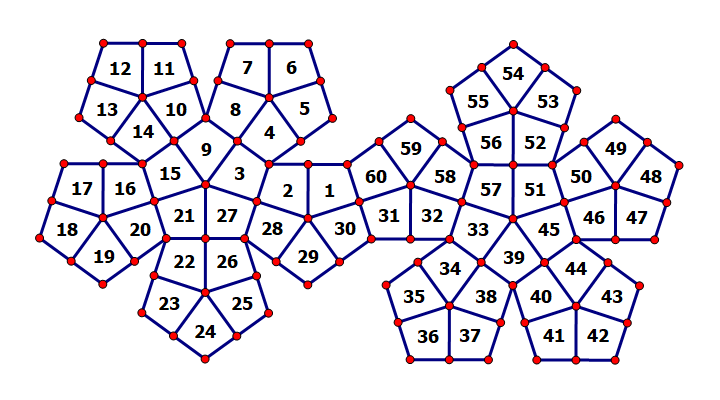
In addition, he thought you might need a plane expansion for better understanding, however, because the plane expansion of a rhombic hexecontahedron is quite unreadable, he left here a modified plane expansion of a regular dodecahedron to illustrate approximately. Hope this image will help you solve this problem.

Wolfram|Alpha Computational Intelligence$^{\mathrm{TM}}$
The rhombic hexecontahedron is a beautiful polyhedron which has $60$ congruent rhombic faces. A rhombic hexecontahedron can be constructed from a regular dodecahedron, by taking its vertices, its face centers and its edge centers and scaling them in or out from the body center to different extents. Also, a rhombic hexecontahedron can be constructed from a regular icosahedron, by appending three rhombuses to each of its faces such that each rhombus shares a vertex with it and every two rhombuses share an edge.
John wants to make some origami of rhombic hexecontahedron. Before getting started from scratch, he was wondering in how many different ways he can make origami of at most $n$ types of colored paper. He has thought for a while and finally determined to leave this problem for you. Furthermore, he added some restriction such that a way of origami is counted if the number of faces colored by the $i$-th type of paper is at least $c_i$ $(i = 1, 2, \cdots, n)$. Of course, the answer might be so large, so you just need to tell him the answer modulo some integer $p$.
Two ways are considered as the same if and only if there exists a way of rotation that can transform one to another so that each corresponding face has the same color. Here is an example of origami after coloring.

Picture from Wolfram Mathworld
In addition, he thought you might need a plane expansion for better understanding, however, because the plane expansion of a rhombic hexecontahedron is quite unreadable, he left here a modified plane expansion of a regular dodecahedron to illustrate approximately. Hope this image will help you solve this problem.

输入解释
The first line contains one integer $T$, indicating the number of test cases.
The following lines describe all the test cases. For each test case:
The first line contains two space-separated integers $n$ and $p$.
The second line contains $n$ space-separated integers $c_1, c_2, \cdots, c_n$.
$1 \leq T \leq 1000$, $1 \leq n \leq 60$, $1 \leq p < 2^{30}
$, $0 \leq c_i \leq 60$ $(i = 1, 2, \cdots, n)$.
It is guaranteed that no more than $100$ test cases satisfy $n > 5$.
The following lines describe all the test cases. For each test case:
The first line contains two space-separated integers $n$ and $p$.
The second line contains $n$ space-separated integers $c_1, c_2, \cdots, c_n$.
$1 \leq T \leq 1000$, $1 \leq n \leq 60$, $1 \leq p < 2^{30}
$, $0 \leq c_i \leq 60$ $(i = 1, 2, \cdots, n)$.
It is guaranteed that no more than $100$ test cases satisfy $n > 5$.
输出解释
For each test case, print the answer modulo $p$ in one line.
输入样例
5 2 1000000007 0 0 2 1000000007 1 0 2 1000000007 0 2 2 1000000007 1 1 5 1000000007 1 1 1 1 1
输出样例
544393230 544393229 544393228 544393228 905148476
来自杭电HDUOJ的附加信息
| Recommend | chendu |
最后修改于 2020-10-25T23:30:38+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 6000/3000MS(Java/Others) | 262144/262144K(Java/Others) |
登陆或注册以提交代码