当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
6354:Everything Has Changed
Special Judge 特殊评判题目描述
Edward is a worker for Aluminum Cyclic Machinery. His work is operating mechanical arms to cut out designed models. Here is a brief introduction of his work.
Assume the operating plane as a two-dimensional coordinate system. At first, there is a disc with center coordinates $(0, 0)$ and radius $R$. Then, $m$ mechanical arms will cut and erase everything within its area of influence simultaneously, the $i$-th area of which is a circle with center coordinates $(x_i, y_i)$ and radius $r_i$ $(i = 1, 2, \cdots, m)$. In order to obtain considerable models, it is guaranteed that every two cutting areas have no intersection and no cutting area contains the whole disc.
Your task is to determine the perimeter of the remaining area of the disc excluding internal perimeter.
Here is an illustration of the sample, in which the red curve is counted but the green curve is not.
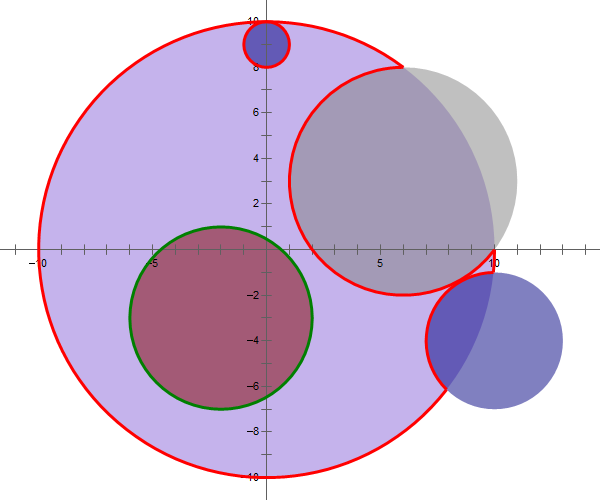
Assume the operating plane as a two-dimensional coordinate system. At first, there is a disc with center coordinates $(0, 0)$ and radius $R$. Then, $m$ mechanical arms will cut and erase everything within its area of influence simultaneously, the $i$-th area of which is a circle with center coordinates $(x_i, y_i)$ and radius $r_i$ $(i = 1, 2, \cdots, m)$. In order to obtain considerable models, it is guaranteed that every two cutting areas have no intersection and no cutting area contains the whole disc.
Your task is to determine the perimeter of the remaining area of the disc excluding internal perimeter.
Here is an illustration of the sample, in which the red curve is counted but the green curve is not.

输入解释
The first line contains one integer $T$, indicating the number of test cases.
The following lines describe all the test cases. For each test case:
The first line contains two integers $m$ and $R$.
The $i$-th line of the following $m$ lines contains three integers $x_i, y_i$ and $r_i$, indicating a cutting area.
$1 \leq T \leq 1000$, $1 \leq m \leq 100$, $-1000 \leq x_i, y_i \leq 1000$, $1 \leq R, r_i \leq 1000$ $(i = 1, 2, \cdots, m)$.
The following lines describe all the test cases. For each test case:
The first line contains two integers $m$ and $R$.
The $i$-th line of the following $m$ lines contains three integers $x_i, y_i$ and $r_i$, indicating a cutting area.
$1 \leq T \leq 1000$, $1 \leq m \leq 100$, $-1000 \leq x_i, y_i \leq 1000$, $1 \leq R, r_i \leq 1000$ $(i = 1, 2, \cdots, m)$.
输出解释
For each test case, print the perimeter of the remaining area in one line. Your answer is considered correct if its absolute or relative error does not exceed $10^{-6}$.
Formally, let your answer be $a$ and the jury's answer be $b$. Your answer is considered correct if $\frac{|a - b|}{\max(1, |b|)} \leq 10^{-6}$.
Formally, let your answer be $a$ and the jury's answer be $b$. Your answer is considered correct if $\frac{|a - b|}{\max(1, |b|)} \leq 10^{-6}$.
输入样例
1 4 10 6 3 5 10 -4 3 -2 -4 4 0 9 1
输出样例
81.62198908430238475376
来自杭电HDUOJ的附加信息
| Recommend | chendu |
最后修改于 2020-10-25T23:30:34+00:00 由爬虫自动更新
共提交 1 次
通过率 0.0%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 262144/262144K(Java/Others) |
登陆或注册以提交代码