当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
6262:Rikka with Mirror
题目描述
Mirror is an indescribable but interesting game on Steam. But this problem is about real mirrors.
Rikka has an $n \times m$ translucent grid, and the side length of each cell is exactly $1$. She can emit light vertically into the grid from the middle of some border cell. After some movement inside the grid, the light will leave the grid from the middle of some other border cell. We can easily calculate the motion length of the light inside the grid.
There are several mirrors inside the grid, the length of each mirror is exactly $\sqrt 2$ . And there are two ways to put mirror: link the left bottom corner and the right top corner, or link the left top corner and the right bottom corner. And if the light reaches a mirror, it will reflect and change the direction, which follows the laws of Physics.
Here is an example.
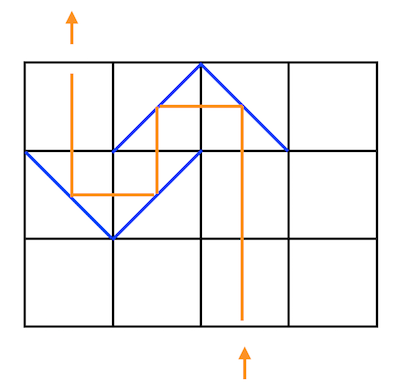
The grid's size is $3 \times 4$, and there are four mirrors inside the grid. If Rikka emits light inside the grid through the middle of the cell $(3,3)$, the light will reach all of the four mirrors and finally go out from the middle of the cell $(1,1)$. The motion length is $7$.
It is clear that Rikka has $2(n+m)$ ways to emit light. Rikka defines the value of the grid as the sum of the motion lengths of all the emitting ways.
Now, Rikka has an $n \times m$ empty grid without any mirror inside it. And she wants to put several mirrors inside some cells of the grid to minimize the value of the grid. (Each cell can only contain at most one mirror). But after some research, Rikka finds that for some cells, the fixing devices break down, i.e., she could not put mirrors inside these cells.
It's a frustrating discovery, so Rikka gives up calculating herself and wants you to help her to get the answer.
Rikka has an $n \times m$ translucent grid, and the side length of each cell is exactly $1$. She can emit light vertically into the grid from the middle of some border cell. After some movement inside the grid, the light will leave the grid from the middle of some other border cell. We can easily calculate the motion length of the light inside the grid.
There are several mirrors inside the grid, the length of each mirror is exactly $\sqrt 2$ . And there are two ways to put mirror: link the left bottom corner and the right top corner, or link the left top corner and the right bottom corner. And if the light reaches a mirror, it will reflect and change the direction, which follows the laws of Physics.
Here is an example.

The grid's size is $3 \times 4$, and there are four mirrors inside the grid. If Rikka emits light inside the grid through the middle of the cell $(3,3)$, the light will reach all of the four mirrors and finally go out from the middle of the cell $(1,1)$. The motion length is $7$.
It is clear that Rikka has $2(n+m)$ ways to emit light. Rikka defines the value of the grid as the sum of the motion lengths of all the emitting ways.
Now, Rikka has an $n \times m$ empty grid without any mirror inside it. And she wants to put several mirrors inside some cells of the grid to minimize the value of the grid. (Each cell can only contain at most one mirror). But after some research, Rikka finds that for some cells, the fixing devices break down, i.e., she could not put mirrors inside these cells.
It's a frustrating discovery, so Rikka gives up calculating herself and wants you to help her to get the answer.
输入解释
The first line contains a single number $t(1 \leq t \leq 100)$, the number of the testcases.
For each testcase, the first line contains two numbers $n,m(1 \leq n \leq 5, 1 \leq m \leq 7)$.
Then $n$ lines follow, each line contains a $01$ string of lenghth $m$. If the $j$th character of the $i$th line is $1$, you can put a mirror inside cell $(i,j)$, otherwise, you can not do this.
The input guarantees that there are at most $2$ testcases with $n=5, m = 7$.
For each testcase, the first line contains two numbers $n,m(1 \leq n \leq 5, 1 \leq m \leq 7)$.
Then $n$ lines follow, each line contains a $01$ string of lenghth $m$. If the $j$th character of the $i$th line is $1$, you can put a mirror inside cell $(i,j)$, otherwise, you can not do this.
The input guarantees that there are at most $2$ testcases with $n=5, m = 7$.
输出解释
For each testcase, output a single line with $n \times m + 1$ integer, the $i$th number is the minimum value of the grid if you put at most $i-1$ mirrors inside it.
输入样例
2 3 3 101 011 101 4 4 1111 1111 1111 1111
输出样例
36 36 36 36 20 20 20 20 20 20 64 64 64 64 40 40 40 40 32 32 32 32 24 24 24 24 24
来自杭电HDUOJ的附加信息
| Recommend | liuyiding |
最后修改于 2020-10-25T23:29:47+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 15000/7500MS(Java/Others) | 512000/512000K(Java/Others) |
登陆或注册以提交代码