当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
5729:Rigid Frameworks
题目描述
Erik Demaine is a Professor in Computer Science at the Massachusetts Institute of Technology. Demaine's research interests range throughout algorithms, from data structures for improving web searches to the geometry of understanding how proteins fold to the computational difficulty of playing games.
Maid xiaodao is learning theoretical computer science in her spare time, and recently she was fascinated by Professor Erik Demaine's Geometric Folding Algorithms - Linkages, Origami, Polyhedra. The following problem was inspired by this book.
Recall that a graph is a collection of vertices and edges connecting the vertices, and that two vertices connected by an edge are called adjacent. Graphs can be embedded in Euclidean space by associating each vertex with a point in the Euclidean space.
$\cdot \ $A flexible graph is an embedding of a graph where it is possible to move one or more vertices continuously so that the distance between at least two nonadjacent vertices is altered while the distances between each pair of adjacent vertices is kept constant.
$\cdot \ $A rigid graph is an embedding of a graph which is not flexible. Informally, a graph is rigid if by replacing the vertices with fully rotating hinges and the edges with rods that are unbending and inelastic, no parts of the graph can be moved independently from the rest of the graph.
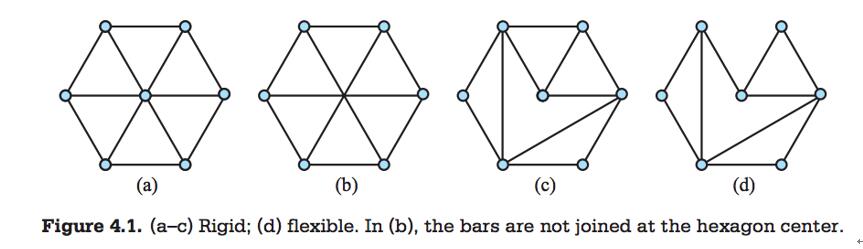
Sit down and relax, to simplify the problem, let's only consider the planar graphs as grids. The grid graphs embedded in the Euclidean plane are not rigid, as the following animation demonstrates:
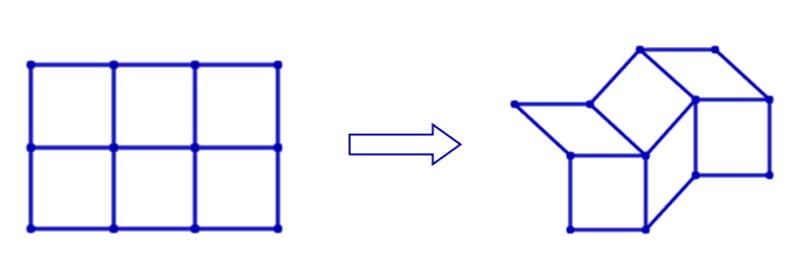
However, one can make them rigid by adding diagonal edges to the cells. For example, the following picture shows a 2 × 3 grid graph.
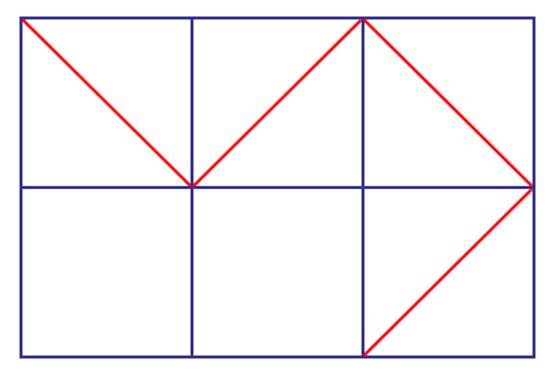
Note that you can add at most one orientation of a diagonal edge in one single cell. In fact, there are 448 ways to make a 2 × 3 grid graph rigid. And now we want to know, how many different rigid m × n grid graph with diagonal edges in total? Dear contestant, could you please find it out?
Maid xiaodao is learning theoretical computer science in her spare time, and recently she was fascinated by Professor Erik Demaine's Geometric Folding Algorithms - Linkages, Origami, Polyhedra. The following problem was inspired by this book.
Recall that a graph is a collection of vertices and edges connecting the vertices, and that two vertices connected by an edge are called adjacent. Graphs can be embedded in Euclidean space by associating each vertex with a point in the Euclidean space.
$\cdot \ $A flexible graph is an embedding of a graph where it is possible to move one or more vertices continuously so that the distance between at least two nonadjacent vertices is altered while the distances between each pair of adjacent vertices is kept constant.
$\cdot \ $A rigid graph is an embedding of a graph which is not flexible. Informally, a graph is rigid if by replacing the vertices with fully rotating hinges and the edges with rods that are unbending and inelastic, no parts of the graph can be moved independently from the rest of the graph.

Sit down and relax, to simplify the problem, let's only consider the planar graphs as grids. The grid graphs embedded in the Euclidean plane are not rigid, as the following animation demonstrates:

However, one can make them rigid by adding diagonal edges to the cells. For example, the following picture shows a 2 × 3 grid graph.

Note that you can add at most one orientation of a diagonal edge in one single cell. In fact, there are 448 ways to make a 2 × 3 grid graph rigid. And now we want to know, how many different rigid m × n grid graph with diagonal edges in total? Dear contestant, could you please find it out?
输入解释
There are multiple test cases. For each test case, the first line contains two integer m and n $(1 \leq m, n \leq 10)$ represented the size of the grid graph.
输出解释
For each test case, output one integer number in a single line — the number of different rigid m × n grid graph with diagonal edges. The answer could be very large, output it modulo $1000000007 (10^{9}+7)$.
输入样例
1 2 3 2 7 9 10 10
输出样例
4 448 357533852 935300639
来自杭电HDUOJ的附加信息
| Author | HIT |
| Recommend | wange2014 |
最后修改于 2020-10-25T23:25:09+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 65536/65536K(Java/Others) |
登陆或注册以提交代码