当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
5518:John's Fences
题目描述
Farmer John built $n$ fences on his farm. The $i$-th fence is a line segment in the plane
whose two endpoints are $(x_{1i}, y_{1i})$ and $(x_{2i}, y_{2i})$. Two different fences
can only intersect at their endpoints.
The following picture shows an example layout of fences.
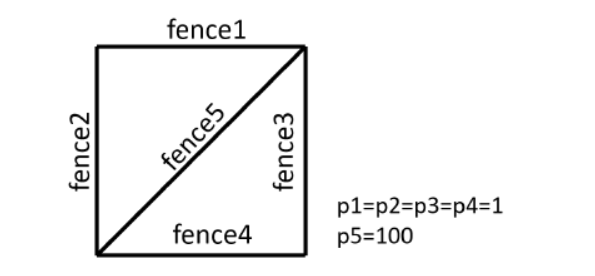
To make cows happy, John will decorate the fences with rope lights.
A fence can hang several rope lights paralleling to itself.
However, a light can not be used alone.
John can only make a decoration by using some lights together (we call it a string of lights) and these lights will form a circle to decorate some fences (a light corresponds to a fence).
In the example, he can use three lights decorate three fences numbered $1, 2, 5$ which form a circle.
A string of lights which decorate fences numbered $k_1,k_2,\cdots,k_m$ costs John $\sum_{i=1}^m p_{k_i}$ dollars. The total cost is the sum of costs of each string. Notice that the cost for more than one strings of lights should be accumulated.
In the example, suppose that he decorate the fences with two strings of lights. One string decorate three fences numbered $1, 2, 5$ and the other string decorate three fences numbered $1, 2, 3, 4$. Then the total cost should be $2\times p_1+2\times p_2+p_3+p_4+p_5 = 106$ dollars.
John can control the switch of each string of lights. He can switch on all lights on that string or switch off
all of them, but he cannot switch on some of they while keeping other lights on that string switched off.
For a fence, if even number of strings on it are switched on, then all the lights on that fence will not work; otherwise,
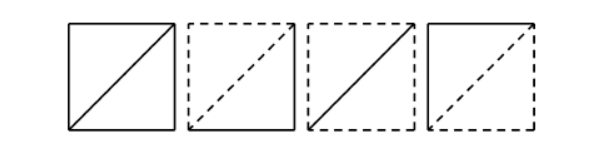
all of them work. We define the shape of lights as a combination of status of each fence (considering the fences lit or not). A shape of lights might be achieved by arrangements of lights. The following picture shows all possible shape of
lights in the example. (Dash lines stands for fences where lights work and the solid stands for fences where lights
don't work.)
The cows love lights, but they are fickle too. They want the lights arranged to form
different shapes from day to day, so John need to make arrangement for decorations so that every possible shapes can be formed by switching on some of the strings of lights and switching off the others.
What is the minimum money John must spend to meet needs of cows.
In the example, he can decorate the fences with two strings of lights.
One string decorate three fences numbered $1, 2, 5$ and the other string decorate three fences numbered $1, 2, 3, 4$.
If he switch off all strings, then cows can get the first shape; if he switch on all strings, then cows can get the last shape; if he switch on only the first string, then then cows can get the third shape; if he switch on only the second string, then then cows can get the second shape. Thus, he can spend 106 dollars to meet need of cows, and it also
turns out to be the minimum cost.
whose two endpoints are $(x_{1i}, y_{1i})$ and $(x_{2i}, y_{2i})$. Two different fences
can only intersect at their endpoints.
The following picture shows an example layout of fences.

To make cows happy, John will decorate the fences with rope lights.
A fence can hang several rope lights paralleling to itself.
However, a light can not be used alone.
John can only make a decoration by using some lights together (we call it a string of lights) and these lights will form a circle to decorate some fences (a light corresponds to a fence).
In the example, he can use three lights decorate three fences numbered $1, 2, 5$ which form a circle.
A string of lights which decorate fences numbered $k_1,k_2,\cdots,k_m$ costs John $\sum_{i=1}^m p_{k_i}$ dollars. The total cost is the sum of costs of each string. Notice that the cost for more than one strings of lights should be accumulated.
In the example, suppose that he decorate the fences with two strings of lights. One string decorate three fences numbered $1, 2, 5$ and the other string decorate three fences numbered $1, 2, 3, 4$. Then the total cost should be $2\times p_1+2\times p_2+p_3+p_4+p_5 = 106$ dollars.
John can control the switch of each string of lights. He can switch on all lights on that string or switch off
all of them, but he cannot switch on some of they while keeping other lights on that string switched off.
For a fence, if even number of strings on it are switched on, then all the lights on that fence will not work; otherwise,
all of them work. We define the shape of lights as a combination of status of each fence (considering the fences lit or not). A shape of lights might be achieved by arrangements of lights. The following picture shows all possible shape of
lights in the example. (Dash lines stands for fences where lights work and the solid stands for fences where lights
don't work.)

The cows love lights, but they are fickle too. They want the lights arranged to form
different shapes from day to day, so John need to make arrangement for decorations so that every possible shapes can be formed by switching on some of the strings of lights and switching off the others.
What is the minimum money John must spend to meet needs of cows.
In the example, he can decorate the fences with two strings of lights.
One string decorate three fences numbered $1, 2, 5$ and the other string decorate three fences numbered $1, 2, 3, 4$.
If he switch off all strings, then cows can get the first shape; if he switch on all strings, then cows can get the last shape; if he switch on only the first string, then then cows can get the third shape; if he switch on only the second string, then then cows can get the second shape. Thus, he can spend 106 dollars to meet need of cows, and it also
turns out to be the minimum cost.
输入解释
The first line contains an integer $t~(1\le t\le 8)$, meaning the total number of test cases.
For each test case, the first line of input contains $n~(1\le n\le 1000)$. The following $n$ lines describe the fences and each line will contain five space separated integers $x_{1i}$, $y_{1i}$, $x_{2i}$, $y_{2i}$ and $p_i$, where $|x_{1i}|,|y_{1i}|,|x_{2i}|,|y_{2i}|\le 10^9$ and $1\le p_i\le 10^5$.
For each test case, the first line of input contains $n~(1\le n\le 1000)$. The following $n$ lines describe the fences and each line will contain five space separated integers $x_{1i}$, $y_{1i}$, $x_{2i}$, $y_{2i}$ and $p_i$, where $|x_{1i}|,|y_{1i}|,|x_{2i}|,|y_{2i}|\le 10^9$ and $1\le p_i\le 10^5$.
输出解释
For each test case, output one integer, which is the minimum money John should spend.
输入样例
2 5 0 0 0 1 1 0 0 1 0 1 0 1 1 1 1 1 0 1 1 1 1 0 0 1 100 9 1 1 3 1 1 1 1 1 3 2 3 1 3 3 2 1 3 3 3 1 1 1 2 2 2 2 2 3 3 3 3 1 2 2 1 2 2 1 3 2 4 1 5 1 4
输出样例
Case #1: 106 Case #2: 22
来自杭电HDUOJ的附加信息
| Recommend | wange2014 |
最后修改于 2020-10-25T23:23:22+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 8000/4000MS(Java/Others) | 65536/65536K(Java/Others) |
登陆或注册以提交代码