当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
5097:Page Rank
题目描述
Evaluation and rank of web pages is a hot topic for many internet companies and researchers. PageRank is a link analysis tool and it assigns a numerical weighting to each element of a hyperlinked set of documents, such as the World Wide Web, with the purpose of "measuring" its relative importance within the set. The algorithm may be applied to any collection of entities with reciprocal quotations and references. The numerical weight that it assigns to any given element E is referred to as the PageRank of E and denoted by . Other factors like Author Rank can contribute to the importance of an entity.
For simplicity, in this problem PageRank vector q is defined as q = Gq, Where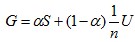 , S is the destination-by-source stochastic matrix, U is all one matrix, n is the number of nodes and α is the weight between 0 and 1 (here we use 0.85).
, S is the destination-by-source stochastic matrix, U is all one matrix, n is the number of nodes and α is the weight between 0 and 1 (here we use 0.85).
For the example on the right, we have:

Denote the current PageRank vector and the next PageRank vector by qcur and qnext respectively. The process is to compute the iterative powering for finding the first eigenvector.
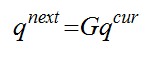
The computation ends until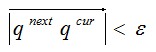 for some small ε(10-10).
for some small ε(10-10).
For simplicity, in this problem PageRank vector q is defined as q = Gq, Where
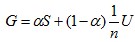 , S is the destination-by-source stochastic matrix, U is all one matrix, n is the number of nodes and α is the weight between 0 and 1 (here we use 0.85).
, S is the destination-by-source stochastic matrix, U is all one matrix, n is the number of nodes and α is the weight between 0 and 1 (here we use 0.85).For the example on the right, we have:

Denote the current PageRank vector and the next PageRank vector by qcur and qnext respectively. The process is to compute the iterative powering for finding the first eigenvector.
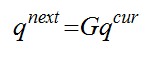
The computation ends until
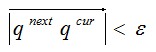 for some small ε(10-10).
for some small ε(10-10).输入解释
The input contains many test cases.
For each case, there are multiple lines. The first line contains an integer N(N<=3000), which represents the number of pages. Then a N*N zero-one matrix follows. The element Eij (0 <= i, j < N) on the matrix represents whether the i-th page has a hyper link to the j-th page.
For each case, there are multiple lines. The first line contains an integer N(N<=3000), which represents the number of pages. Then a N*N zero-one matrix follows. The element Eij (0 <= i, j < N) on the matrix represents whether the i-th page has a hyper link to the j-th page.
输出解释
Output one line with the eigenvector. The numbers should be separated by a space and be correctly rounded to two decimal places.
输入样例
4 0111 0011 0001 0100
输出样例
0.15 1.49 0.83 1.53
来自杭电HDUOJ的附加信息
| Recommend | hujie |
最后修改于 2020-10-25T23:19:46+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 3000/1500MS(Java/Others) | 100000/100000K(Java/Others) |
登陆或注册以提交代码