当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
5051:Fraction
题目描述
Given a number n, and a geometric progression ai = b * qi, i ≥ 0, what is the fraction of the elements of that progression with decimal notation that has the decimal notation of n as prefix ?
More formally, if ci out of the first i elements of the progression start with n in decimal notation, you need to find the limit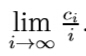 . It is guaranteed that the limit always exists.
. It is guaranteed that the limit always exists.
For example, n = 7, b = 1, q = 2. About 5.799% of all powers of two start with 7. (the smallest one is 246 = 70368744177664)
More formally, if ci out of the first i elements of the progression start with n in decimal notation, you need to find the limit
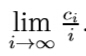 . It is guaranteed that the limit always exists.
. It is guaranteed that the limit always exists.For example, n = 7, b = 1, q = 2. About 5.799% of all powers of two start with 7. (the smallest one is 246 = 70368744177664)
输入解释
The first line of the input is T (1 ≤ T ≤ 100), which stands for the number of test cases you need to solve.
Each case contains three integers n,b and q. (1 ≤ n, b, q ≤ 1000)
Each case contains three integers n,b and q. (1 ≤ n, b, q ≤ 1000)
输出解释
For each test case, print a line “Case #t: ”(without quotes, t means the index of the test case) at the beginning. Then output one floating number – the sought fraction. Round your answer to the 5th decimal place.
输入样例
2 7 1 2 1 1 1
输出样例
Case #1: 0.05799 Case #2: 1.00000
来自杭电HDUOJ的附加信息
| Recommend | hujie |
最后修改于 2020-10-25T23:19:17+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 65536/65536K(Java/Others) |
登陆或注册以提交代码