当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
4728:A Game in the Hospital
题目描述
Mzry1992 got sick recently. He had to go to the hospital for treatment. The time in the hospital was very boring, so Mzry1992 designed a game and wanted to persuade the nurse to play with him.
The game is played as follows: There are n piles of candies on the table. Each pile has a certain number of candies. Mzry1992 and the nurse take turns to eat candies. As the designed of the game, Mzry1992 always starts first. When it's someone's turn to eat candies, he must select a pile of candies (suppose the pile has m candies now), and eat x(0 < x <= ) candies. Otherwise, he loses the game.
) candies. Otherwise, he loses the game.
(" " indicates the largest integer which is not greater than x)
" indicates the largest integer which is not greater than x)
The nurse loved candies, so she agreed to play with Mzry1992. To start the game, they began to prepare n candy piles. After they had arranged the first n-1 piles of candies (where the number of candies in the ith pile was xi, 1 <= i <= n - 1), a new patient came in and the nurse had to go to take care of him. So Mzry1992 was left alone to decide the number of candies in the last pile.
But before the nurse left, she demanded that the last pile must have no less than L candies and no more than R candies, i.e. , L <= xn <= R.
Mzry1992 agreed with the nurse's demand, since it would be unfair for the nurse if Mzry1992 could place any number of candies in the last pile. Now Mzry1992 wondered, if both he and the nurse play with their best strategies, how many different ways of placing candies in the last pile will make him lose?
The game is played as follows: There are n piles of candies on the table. Each pile has a certain number of candies. Mzry1992 and the nurse take turns to eat candies. As the designed of the game, Mzry1992 always starts first. When it's someone's turn to eat candies, he must select a pile of candies (suppose the pile has m candies now), and eat x(0 < x <=
 ) candies. Otherwise, he loses the game.
) candies. Otherwise, he loses the game.("
 " indicates the largest integer which is not greater than x)
" indicates the largest integer which is not greater than x)The nurse loved candies, so she agreed to play with Mzry1992. To start the game, they began to prepare n candy piles. After they had arranged the first n-1 piles of candies (where the number of candies in the ith pile was xi, 1 <= i <= n - 1), a new patient came in and the nurse had to go to take care of him. So Mzry1992 was left alone to decide the number of candies in the last pile.
But before the nurse left, she demanded that the last pile must have no less than L candies and no more than R candies, i.e. , L <= xn <= R.
Mzry1992 agreed with the nurse's demand, since it would be unfair for the nurse if Mzry1992 could place any number of candies in the last pile. Now Mzry1992 wondered, if both he and the nurse play with their best strategies, how many different ways of placing candies in the last pile will make him lose?
输入解释
The first line has a number T (T <= 20) , indicating the number of test cases.
Then there comes the input of each test case.
The input of each test case has four lines.
The first line contains three integers A, B, and C(0 <= A,B <= 1018, 1 <= C <= 1018), which are defined above in the description.
The second line contains an integer n(1 <= n <= 10), indicating the number of candy piles.
The third line contains n - 1 integers x1, x2, ... , xn-1, where xi(1 <= xi <= 1018) indicates the number of candies in the ith pile.
The fourth line contains two integers L and R(1 <= L <= R <= 1018), which constrains the number of the nth pile in the range [L, R], i.e., L <= xn <= R.
We can guaranteed that at any time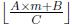 will no more than 105.
will no more than 105.
Then there comes the input of each test case.
The input of each test case has four lines.
The first line contains three integers A, B, and C(0 <= A,B <= 1018, 1 <= C <= 1018), which are defined above in the description.
The second line contains an integer n(1 <= n <= 10), indicating the number of candy piles.
The third line contains n - 1 integers x1, x2, ... , xn-1, where xi(1 <= xi <= 1018) indicates the number of candies in the ith pile.
The fourth line contains two integers L and R(1 <= L <= R <= 1018), which constrains the number of the nth pile in the range [L, R], i.e., L <= xn <= R.
We can guaranteed that at any time
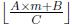 will no more than 105.
will no more than 105.输出解释
For every case, you should output "Case #t: " at first, without quotes. The t is the case number starting from 1.
Then follows the answer. which indicates the number of different ways of placing candies in the nth pile that will make Mzry1992 lose.
Then follows the answer. which indicates the number of different ways of placing candies in the nth pile that will make Mzry1992 lose.
输入样例
1 1 2 3 3 3 4 1 8
输出样例
Case #1: 1
来自杭电HDUOJ的附加信息
| Recommend | liuyiding |
最后修改于 2020-10-25T23:16:14+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码