当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
4636:Painting the Football
题目描述
The football, well known as a worldwide popular sport, is made of 12 regular pentagons and 20 regular hexagons.

In this problem, L has to color a new football. The football is totally white in the beginning and L has to color some of its faces into black (maybe zero). Look at the picture below, the 32 faces of a football are numbered from 1 to 32. Two faces are considered connected if and only if they share a same side such like 12 and 13 as well as 29 and 30. Each step L can choose some connected faces of the football and color all these faces into black or white no matter what color it used to be. For example, L can color the faces 2, 3, 4 and 5 at the same time, but he can’t color the faces 26 and 29 at the same time.
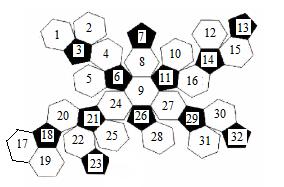
Now give the target state of the football, your task is calculating the minimum steps that L needs to do.

In this problem, L has to color a new football. The football is totally white in the beginning and L has to color some of its faces into black (maybe zero). Look at the picture below, the 32 faces of a football are numbered from 1 to 32. Two faces are considered connected if and only if they share a same side such like 12 and 13 as well as 29 and 30. Each step L can choose some connected faces of the football and color all these faces into black or white no matter what color it used to be. For example, L can color the faces 2, 3, 4 and 5 at the same time, but he can’t color the faces 26 and 29 at the same time.

Now give the target state of the football, your task is calculating the minimum steps that L needs to do.
输入解释
The first line of the date is an integer T, which is the number of the text cases.
Then T cases follow describe a target state. Each case contains 32 integers in a line. If the ith number in this line is 1, it means that the face with index i need to color to black, otherwise it need to color to white.
Then T cases follow describe a target state. Each case contains 32 integers in a line. If the ith number in this line is 1, it means that the face with index i need to color to black, otherwise it need to color to white.
输出解释
For each test case, output the case number first, then output minimum steps L needs to do to color the football to the target state.
输入样例
2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 0 0 1 1 0 0 0 1 0 1 1 0 0 0 1 0 0 1 0 1 0 0 1 0 0 1 0 0 1
输出样例
Case 1: 1 Case 2: 2
提示
Some useful information: In the original football, the face 1 and face 13 is connected, the face 13 and face 17 are connected, the face 17 and face 32 are connected, the face 15 and face 32 are connected and the face 19 and face 32 are connected. If you are still lack of imagination, maybe the follow links may help you: http://www1.esgweb.net/Article/UploadFiles09/200810/2008101900394743.gif http://www1.esgweb.net/Article/UploadFiles09/200810/2008101900394998.gif http://www.3dcadbrowser.com/download.aspx?3dmodel=21288
来自杭电HDUOJ的附加信息
| Recommend | zhuyuanchen520 |
最后修改于 2020-10-25T23:15:22+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码