当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
4210:Su-domino-ku
题目描述
As if there were not already enough sudoku-like puzzles, the July 2009 issue of Games Magazine describes the following variant that combines facets of both sudoku and dominos. The puzzle is a form of a standard sudoku, in which there is a nine-by-nine grid that must be filled in using only digits 1 through 9. In a successful solution:
Each row must contain each of the digits 1 through 9.
Each column must contain each of the digits 1 through 9.
Each of the indicated three-by-three squares must contain each of the digits 1 through 9.
For a su-domino-ku, nine arbitrary cells are initialized with the numbers 1 to 9. This leaves 72 remaining cells. Those must be filled by making use of the following set of 36 domino tiles. The tile set includes one domino for each possible pair of unique numbers from 1 to 9 (e.g., 1+2, 1+3, 1+4, 1+5, 1+6, 1+7, 1+8, 1+9, 2+3, 2+4, 2+5, ...). Note well that there are not separate 1+2 and 2+1 tiles in the set; the single such domino can be rotated to provide either orientation. Also, note that dominos may cross the boundary of the three-by-three squares (as does the 2+9 domino in our coming example).
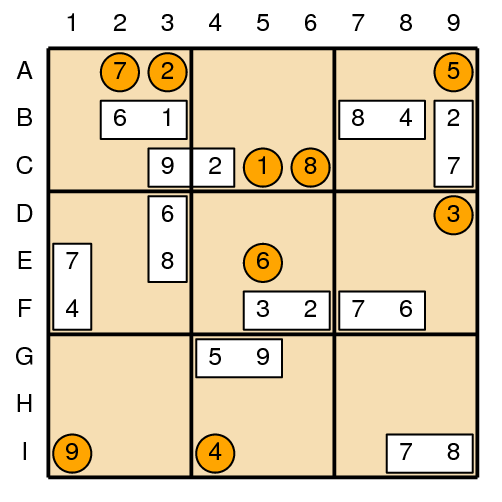
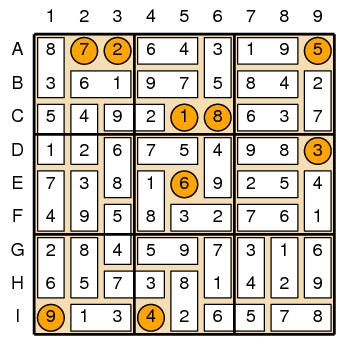
To help you out, we will begin each puzzle by identifying the location of some of the dominos. For example, Figure 1 shows a sample puzzle in its initial state. Figure 2 shows the unique way to complete that puzzle.
Each row must contain each of the digits 1 through 9.
Each column must contain each of the digits 1 through 9.
Each of the indicated three-by-three squares must contain each of the digits 1 through 9.
For a su-domino-ku, nine arbitrary cells are initialized with the numbers 1 to 9. This leaves 72 remaining cells. Those must be filled by making use of the following set of 36 domino tiles. The tile set includes one domino for each possible pair of unique numbers from 1 to 9 (e.g., 1+2, 1+3, 1+4, 1+5, 1+6, 1+7, 1+8, 1+9, 2+3, 2+4, 2+5, ...). Note well that there are not separate 1+2 and 2+1 tiles in the set; the single such domino can be rotated to provide either orientation. Also, note that dominos may cross the boundary of the three-by-three squares (as does the 2+9 domino in our coming example).
To help you out, we will begin each puzzle by identifying the location of some of the dominos. For example, Figure 1 shows a sample puzzle in its initial state. Figure 2 shows the unique way to complete that puzzle.


输入解释
Each puzzle description begins with a line containing an integer N, for 10 ≤ N ≤ 35, representing the number of dominos that are initially placed in the starting configuration. Following that are N lines, each describing a single domino as U LU V LV. Value U is one of the numbers on the domino, and LU is a two-character string representing the location of value U on the board based on the grid system diagrammed in Figure 1. The variables V and LV representing the respective value and location of the other half of the domino. For example, our first sample input beings with a domino described as 6 B2 1 B3. This corresponds to the domino with values 6+1 being placed on the board such that value 6 is in row B, column 2 and value 1 in row B, column 3. The two locations for a given domino will always be neighboring.
After the specification of the N dominos will be a final line that describes the initial locations of the isolated numbers, ordered from 1 to 9, using the same row-column conventions for describing locations on the board. All initial numbers and dominos will be at unique locations.
The input file ends with a line containing 0.
After the specification of the N dominos will be a final line that describes the initial locations of the isolated numbers, ordered from 1 to 9, using the same row-column conventions for describing locations on the board. All initial numbers and dominos will be at unique locations.
The input file ends with a line containing 0.
输出解释
For each puzzle, output an initial line identifying the puzzle number, as shown below. Following that, output the 9x9 sudoku board that can be formed with the set of dominos. There will be a unique solution for each puzzle.
输入样例
10 6 B2 1 B3 2 C4 9 C3 6 D3 8 E3 7 E1 4 F1 8 B7 4 B8 3 F5 2 F6 7 F7 6 F8 5 G4 9 G5 7 I8 8 I9 7 C9 2 B9 C5 A3 D9 I4 A9 E5 A2 C6 I1 11 5 I9 2 H9 6 A5 7 A6 4 B8 6 C8 3 B5 8 B4 3 C3 2 D3 9 D2 8 E2 3 G2 5 H2 1 A2 8 A1 1 H8 3 I8 8 I3 7 I4 4 I6 9 I7 I5 E6 D1 F2 B3 G9 H7 C9 E5 0
输出样例
Puzzle 1 872643195 361975842 549218637 126754983 738169254 495832761 284597316 657381429 913426578 Puzzle 2 814267593 965831247 273945168 392176854 586492371 741358629 137529486 459683712 628714935
来自杭电HDUOJ的附加信息
| Recommend | lcy |
最后修改于 2020-10-25T23:11:18+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 4000/1500MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码