当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
4131:Fraction Tree
题目描述
Fraction Tree ,alse called Stern-Brocot Tree.It's a beautiful way to construct the set of all nonnegative fractions.The idea is to start with irreducible fractions representing zero and infinity,
1/0 0/1
and then between adjacent fractions n/m and n'/m' we insert fraction (n+n')/ (m+m'), then we obtain
1/0 1/1 0/1
Repeating the process, we get
1/0 2/1 1/1 1/2 0/1
and then
1/0 3/1 2/1 3/2 1/1 2/3 1/2 1/3 0/1
and so forth. It can be proven that every irreducible fraction appears at some iteration and no fraction ever appears twice . The process can be represented graphically:
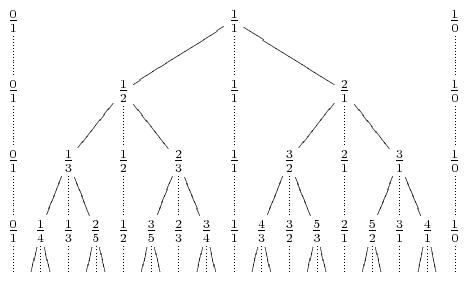
We can,in fact,regard the Stern-Brocot Tree as a number system for representing rational numbers,because each positive,reduced fractio occurs exactly once.Let's use the letters L and R to stand for going down to the left or right branch as we proceed from the root of the tree to a particular fraction; then a string of L's and R's uniquely identifies a place in the tree.For example,LRRL means that we go left from 1/1 down to 1/2,then right to 2/3,then right to 3/4,then left to 5/7.We can consider LRRL to be a representatio of 5/7. Every positive fraction gets represented in this way as a unique string of L's and R's.
There are two natural questios:
(1)Given positive integers m and n (m is coprime with n).what's the string of L's and R's that corresponds to m/n?
(2)Given a string of L's and R's,what fraction corresponds to it?
Now you need to write a problem to solve them.
1/0 0/1
and then between adjacent fractions n/m and n'/m' we insert fraction (n+n')/ (m+m'), then we obtain
1/0 1/1 0/1
Repeating the process, we get
1/0 2/1 1/1 1/2 0/1
and then
1/0 3/1 2/1 3/2 1/1 2/3 1/2 1/3 0/1
and so forth. It can be proven that every irreducible fraction appears at some iteration and no fraction ever appears twice . The process can be represented graphically:

We can,in fact,regard the Stern-Brocot Tree as a number system for representing rational numbers,because each positive,reduced fractio occurs exactly once.Let's use the letters L and R to stand for going down to the left or right branch as we proceed from the root of the tree to a particular fraction; then a string of L's and R's uniquely identifies a place in the tree.For example,LRRL means that we go left from 1/1 down to 1/2,then right to 2/3,then right to 3/4,then left to 5/7.We can consider LRRL to be a representatio of 5/7. Every positive fraction gets represented in this way as a unique string of L's and R's.
There are two natural questios:
(1)Given positive integers m and n (m is coprime with n).what's the string of L's and R's that corresponds to m/n?
(2)Given a string of L's and R's,what fraction corresponds to it?
Now you need to write a problem to solve them.
输入解释
The first line of input contains a single integer T - a number of test cases.
Each of the next T(T <= 1000) lines begin with a integer K(which kind of probrlem),if K = 1,following two integers M and N(M,N <= 1000000).else following a string of L's and R's(length <= 10).
Each of the next T(T <= 1000) lines begin with a integer K(which kind of probrlem),if K = 1,following two integers M and N(M,N <= 1000000).else following a string of L's and R's(length <= 10).
输出解释
For each set of data the program prints the answer.
输入样例
2 1 5 7 2 LRRL
输出样例
LRRL 5 7
来自杭电HDUOJ的附加信息
| Recommend | lcy |
最后修改于 2020-10-25T23:10:33+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码