当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
3889:Statistical Problems
题目描述
Last year Dige was having a statistic course and had to solve many problems and calculate many results. However, he thought it was worthless to practice that much since that after solving several problems, the rest was just repeating and repeating, which is too simple, sometimes naive. Therefore, he wanted someone to help him write a program, which would output all the results he needs immediately instead of calculating them himself.
The statistic problems might include z-scores, one-sample t-tests, correlation and regression.
For a population of real numbers, the standard deviation (SD) of the numbers is defined as

You know, sometimes (almost always) we cannot get data for a whole population, and what we’ve got is just a sample from it. For a sample from a population, the SD is


There are many ways to calculate a correlation coefficient between two variables X and Y, and one of the most popular one is Pearson’s r, which is
It is a little complicated for regression, which is meant to find the “best” a and b for the estimation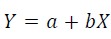


The statistic problems might include z-scores, one-sample t-tests, correlation and regression.
For a population of real numbers, the standard deviation (SD) of the numbers is defined as


You know, sometimes (almost always) we cannot get data for a whole population, and what we’ve got is just a sample from it. For a sample from a population, the SD is



There are many ways to calculate a correlation coefficient between two variables X and Y, and one of the most popular one is Pearson’s r, which is

It is a little complicated for regression, which is meant to find the “best” a and b for the estimation
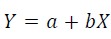


输入解释
Inputs include multiple cases (no more than 100) and would end with EOF.
Each case starts with a line including two integers p and n. p indicates the kind of problem to solve, 1 means z-score, 2 means one-sample t-test, 3 means Pearson correlation, 4 means regression. n is the number of data points. n is no smaller than 2 and no larger than 10000.
If p is 1, then the following input of the case would be n numbers.
If p is 2, then the following input of the case would be (n + 1) numbers, the first one is the mean of the population and the rest are the data of the sample.
If p is 3 or 4, then the following input of the case would be 2 lines, each with n numbers. The first line are Xs and the second are Ys.
Note that inputs can be separated not only by spaces, but also tabs and new lines, or even combinations of them.
Each case starts with a line including two integers p and n. p indicates the kind of problem to solve, 1 means z-score, 2 means one-sample t-test, 3 means Pearson correlation, 4 means regression. n is the number of data points. n is no smaller than 2 and no larger than 10000.
If p is 1, then the following input of the case would be n numbers.
If p is 2, then the following input of the case would be (n + 1) numbers, the first one is the mean of the population and the rest are the data of the sample.
If p is 3 or 4, then the following input of the case would be 2 lines, each with n numbers. The first line are Xs and the second are Ys.
Note that inputs can be separated not only by spaces, but also tabs and new lines, or even combinations of them.
输出解释
For each case, print the output in one line, round all numbers to 2 decimal points, and separate them with spaces.
If p is 1, you should output the z-score for each number without changing their orders.
If p is 2, you should output the t-value.
If p is 3 or 4, output the Pearson’s r for them if p is 3, or a and b as is mentioned above if p is 4.
If p is 1, you should output the z-score for each number without changing their orders.
If p is 2, you should output the t-value.
If p is 3 or 4, output the Pearson’s r for them if p is 3, or a and b as is mentioned above if p is 4.
输入样例
1 3 1 2 3 1 2 1 2 2 3 2 1 2 3 3 4 1 2 3 4 5 6 7 8 4 3 1 2 3 3 5 7
输出样例
-1.22 0.00 1.22 -1.00 1.00 0.00 1.00 1.00 2.00
提示
Output -0.00 as it is.
来自杭电HDUOJ的附加信息
| Author | Entheos |
| Recommend | lcy |
最后修改于 2020-10-25T23:07:58+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 6000/2000MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码