当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
3758:Factorial Simplification
题目描述
Peter is working on a combinatorial problem. He has carried out quite lengthy derivations and got a resulting formula that is a ratio of two products of factorials like this:
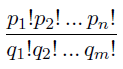
This does not surprise Peter, since factorials appear quite often in various combinatorial formulae, because n! represents the number of transpositions of n elements - one of the basic combinatorial objects.
However, Peter might have made a mistake in his derivations. He knows that the result should be an integer number and he needs to check this first. For an integer result Peter wants to simplify this formula to get a better feeling of its actual combinatorial significance. He wants to represent the same number as a product of factorials like this.
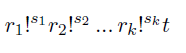
where all ri are distinct integer numbers greater than one in the descending order (ri > ri+1 > 1), si and t are positive integers. Among all the possible representations in this form, Peter is interested in one where r1 is the largest possible number, among those in the one where s1 is the largest possible number; among those in the one where r2 is the largest possible number; among those in the one where s2 is the largest possible number; etc, until the remaining t cannot be further represented in this form. Peter does not care about the actual value of t. He wants to know what is the factorial-product part of his result.
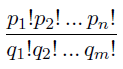
This does not surprise Peter, since factorials appear quite often in various combinatorial formulae, because n! represents the number of transpositions of n elements - one of the basic combinatorial objects.
However, Peter might have made a mistake in his derivations. He knows that the result should be an integer number and he needs to check this first. For an integer result Peter wants to simplify this formula to get a better feeling of its actual combinatorial significance. He wants to represent the same number as a product of factorials like this.
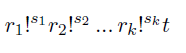
where all ri are distinct integer numbers greater than one in the descending order (ri > ri+1 > 1), si and t are positive integers. Among all the possible representations in this form, Peter is interested in one where r1 is the largest possible number, among those in the one where s1 is the largest possible number; among those in the one where r2 is the largest possible number; among those in the one where s2 is the largest possible number; etc, until the remaining t cannot be further represented in this form. Peter does not care about the actual value of t. He wants to know what is the factorial-product part of his result.
输入解释
The input begins with an integer T. The next T blocks each represents a case. The first line of each case contains two integer numbers n and m (1 ≤ n, m ≤ 1000). The second line contains n integer numbers pi (1 ≤ pi ≤ 10 000) separated by spaces. The third line contains m integer numbers qi (1 ≤ qi ≤ 10 000) separated by spaces.
输出解释
For each case, on the first line of the output write a single integer number k. Write k = -1 if the ratio of the given factorial products is not an integer. Write k = 0 if the ratio is an integer but it cannot be represented in the desired form. Write k > 0 followed by k lines if the ratio can be represented by a factorial product as described in the problem statement. On each of the following k lines write two integers ri and si (for i = 1 ... k) separated by a space.
输入样例
3 1 2 6 4 4 1 2 6 3 4 4 2 9 2 2 2 3 4
输出样例
-1 0 2 7 1 2 2
来自杭电HDUOJ的附加信息
| Author | Andrey Stankevich |
| Recommend | notonlysuccess |
最后修改于 2020-10-25T23:06:45+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 4000/2000MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码