当前你的浏览器版本过低，网站已在兼容模式下运行，兼容模式仅提供最小功能支持，网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
3692：Shade of Hallelujah Mountain
题目描述
On the planet Pandora, huge rocks are floating in the sky. Despite the beautiful scenery, these rocks bring some critical problem: they block the sunshine, and shade on the ground. Na'vi ("people" living on the planet) cannot grow plants in the shade because of the lack of sunshine. In order to predicate the amount of food they can get, they have to calculate the area of the shade.
Let’s assume the "sun" as a point-source of light, and the ground as a infinite flat plane. Also, to simplify this problem, assume all rocks are convex polyhedrons.
Now here is a mathematical problem. Given the position of the point-source of light, the position of a convex polyhedron and the position of an infinite plane, you are required to calculate the area of the shade. Please note that light travels in a strictly straight line and the light source and the convex polyhedron are on the same side of the plane. The light source is not placed in the convex polyhedron, nor on the polyhedron or on the plane.
Let’s assume the "sun" as a point-source of light, and the ground as a infinite flat plane. Also, to simplify this problem, assume all rocks are convex polyhedrons.
Now here is a mathematical problem. Given the position of the point-source of light, the position of a convex polyhedron and the position of an infinite plane, you are required to calculate the area of the shade. Please note that light travels in a strictly straight line and the light source and the convex polyhedron are on the same side of the plane. The light source is not placed in the convex polyhedron, nor on the polyhedron or on the plane.
输入解释
The input contains no more than 100 cases.
Each case contains several lines which are formatted as follows.
a b c d
n
x1 y1 z1
x2 y2 z2
......
xn yn zn
x0 y0 z0
a, b, c and d means that the plane is ax+by+cz=d. n means the number of vertex of the convex polyhedron. It is guaranteed that n is no more than 100. Following it are n lines. Each line contains three float numbers, indicating the position of a point which is a vertex of the polyhedron. The last line also contains three float numbers, which means the position of the point-source of light.
The input is ended by a=0, b=0, c=0 and d=0.
Each case contains several lines which are formatted as follows.
a b c d
n
x1 y1 z1
x2 y2 z2
......
xn yn zn
x0 y0 z0
a, b, c and d means that the plane is ax+by+cz=d. n means the number of vertex of the convex polyhedron. It is guaranteed that n is no more than 100. Following it are n lines. Each line contains three float numbers, indicating the position of a point which is a vertex of the polyhedron. The last line also contains three float numbers, which means the position of the point-source of light.
The input is ended by a=0, b=0, c=0 and d=0.
输出解释
For each case, if there is no shade on the plane, print “0.00”.
If the area of the shade is infinite, print “Infi”.
Otherwise, print out the area of the shade. Please round the result to two digits after the decimal point.
Here are some hints to help you implement rotation in 3-dimensional space.
Assume that there is a plane ax+by+cz=0 , and our task is to rotate the whole space so that the plane will be in the position z=0 .
As we all know, the normal vector of the plane is (a,b,c) , so after we rotate the space, the normal vector will be the z-axis. So we can only consider how to rotate the vector to the position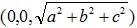
.
We can divide the process into 2 steps. First step, rotate the normal vector to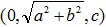
. Second step, rotate 
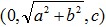to 
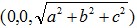. Then apply the two rotation steps on the whole space, we can rotate the plane to a given position.
It is easy to implement the two steps. In first step, the third number in the normal vector does not change, so this is like rotation in a 2-dimensional space. Similarly, we implement the second step.
If the area of the shade is infinite, print “Infi”.
Otherwise, print out the area of the shade. Please round the result to two digits after the decimal point.
Hint
Here are some hints to help you implement rotation in 3-dimensional space.
Assume that there is a plane ax+by+cz=0 , and our task is to rotate the whole space so that the plane will be in the position z=0 .
As we all know, the normal vector of the plane is (a,b,c) , so after we rotate the space, the normal vector will be the z-axis. So we can only consider how to rotate the vector to the position
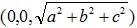.We can divide the process into 2 steps. First step, rotate the normal vector to
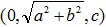. Second step, rotate 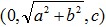to 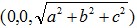. Then apply the two rotation steps on the whole space, we can rotate the plane to a given position.It is easy to implement the two steps. In first step, the third number in the normal vector does not change, so this is like rotation in a 2-dimensional space. Similarly, we implement the second step.
输入样例
0 0 1 0 8 1 1 1 1 -1 1 -1 1 1 -1 -1 1 1 1 0 1 -1 0 -1 1 0 -1 -1 0 2 2 1 1 0 0 -2 8 1 1 1 1 1 -1 1 -1 1 1 -1 -1 -1 1 1 -1 1 -1 -1 -1 1 -1 -1 -1 2 0 0 1 1 1 1 0 0 0 0 0 0 0 0
输出样例
Infi 64.00 0.00
来自杭电HDUOJ的附加信息
| Recommend | axubiao |
最后修改于 2020-10-25T23:06:07+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 65536/32768K(Java/Others) |
登陆或注册以提交代码