当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
3633:Black and white
Special Judge 特殊评判题目描述
Given a partially filled grid with N rows and M columns and each gird with a number.We define sumBlack is the sum of all Black gird and sumWhite is the sum of all White gird.
You are to calculate how many ways there are to fill the remaining part of the grid under the constraints stated below to make the absolute of (sumBlack - sumWhite) minimum and output one of these ways (if any exist).
Each cell in the grid should be colored either black or white.
All black cells in the grid should be connected with each other, and all white cells should also be connected with each other.The pictures below show two filled grids where this constraint is only fulfilled in the picture2.
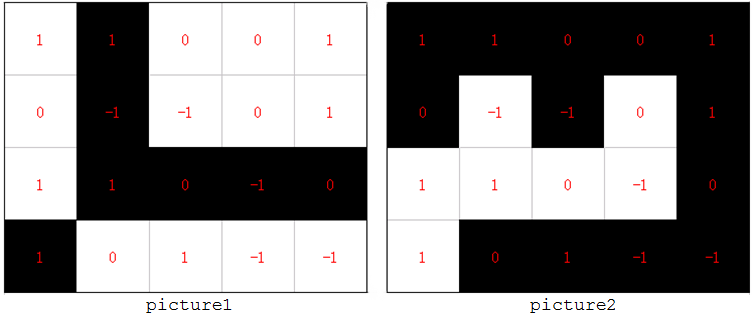
There must be no 2x2 blocks in the grid which consists of only white cells, or of only black cells.
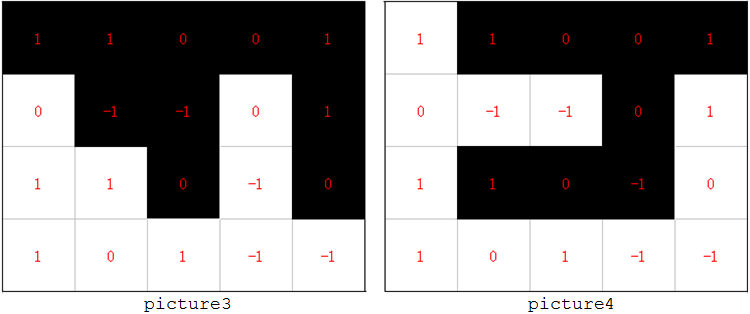
The picture3 shows a grid with a black and a white 2x2 block, while the picture4 contains no such 2x2 block.
You are not allowed to change the color of any of the cells whose color has already been assigned in the input, and all cells must be colored.
You are to calculate how many ways there are to fill the remaining part of the grid under the constraints stated below to make the absolute of (sumBlack - sumWhite) minimum and output one of these ways (if any exist).
Each cell in the grid should be colored either black or white.
All black cells in the grid should be connected with each other, and all white cells should also be connected with each other.The pictures below show two filled grids where this constraint is only fulfilled in the picture2.

There must be no 2x2 blocks in the grid which consists of only white cells, or of only black cells.
The picture3 shows a grid with a black and a white 2x2 block, while the picture4 contains no such 2x2 block.

You are not allowed to change the color of any of the cells whose color has already been assigned in the input, and all cells must be colored.
输入解释
The first line in the input contains an integer T (1<=T<=30), the number of cases to follow.
Each case starts with two integers, N and M (2 ≤ N, M ≤ 8), the number of rows and columns respectively in the grid.
The next N lines contains M characters each and describes the grid using the following characters:
# - a cell which is colored black
o - a cell which is colored white
. - a cell which color has not yet been assigned
The next N lines contains M integers (-1 or 0 or 1) each indicating the number of this gird.
Each case starts with two integers, N and M (2 ≤ N, M ≤ 8), the number of rows and columns respectively in the grid.
The next N lines contains M characters each and describes the grid using the following characters:
# - a cell which is colored black
o - a cell which is colored white
. - a cell which color has not yet been assigned
The next N lines contains M integers (-1 or 0 or 1) each indicating the number of this gird.
输出解释
For each case, first line output the number of case(as shown in the sample output)
If there are at least one way, then output the minimum absolute of (sumBlack - sumWhite) and the number of ways to fill the grid make it minimum in a line and output one of these ways, using the same format for the grid as in the input.(anyone is ok)
If there is no way to fill the gird under the constraints stated , just output two zero.
Output a blank line after each case.(Special judge.If you not output a blank line after each case, you may get Wrong Answer)
If there are at least one way, then output the minimum absolute of (sumBlack - sumWhite) and the number of ways to fill the grid make it minimum in a line and output one of these ways, using the same format for the grid as in the input.(anyone is ok)
If there is no way to fill the gird under the constraints stated , just output two zero.
Output a blank line after each case.(Special judge.If you not output a blank line after each case, you may get Wrong Answer)
输入样例
4 2 3 xxx oox 1 1 0 0 1 0 2 3 ... ... 1 1 0 0 1 -1 5 5 ..x.. ..... ....o o.... .x... 1 1 0 0 1 0 -1 -1 0 1 1 1 0 -1 0 1 0 1 -1 -1 -1 -1 1 -1 0 4 5 ..... ..... ..... ..... 1 1 0 0 1 0 -1 -1 0 1 1 1 0 -1 0 1 0 1 -1 -1
输出样例
Case 1: 1 1 xxx oox Case 2: 0 8 xxx xox Case 3: 0 0 Case 4: 1 54 xxxxx xoxox oooox oxxxx
来自杭电HDUOJ的附加信息
| Author | NotOnlySuccess |
| Recommend | lcy |
最后修改于 2020-10-25T23:05:25+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 20000/10000MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码