当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
3590:PP and QQ
题目描述
PP and QQ were playing games at Christmas Eve. They drew some Christmas trees on a paper:
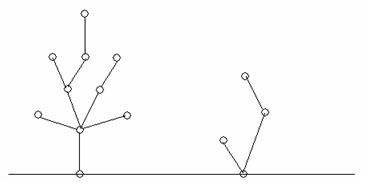
Then they took turns to cut a branch of a tree, and removed the part of the tree which had already not connected with the root. A step shows as follows:
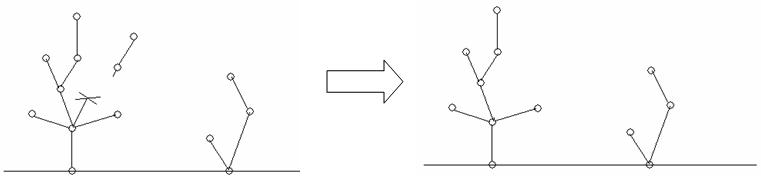
PP always moved first.
PP and QQ took turns (PP was always the first person to move), to cut an edge in the graph, and removed the part of the tree that no longer connected to the root. The person who cannot make a move won the game.
Your job is to decide who will finally win the game if both of them use the best strategy.

Then they took turns to cut a branch of a tree, and removed the part of the tree which had already not connected with the root. A step shows as follows:

PP always moved first.
PP and QQ took turns (PP was always the first person to move), to cut an edge in the graph, and removed the part of the tree that no longer connected to the root. The person who cannot make a move won the game.
Your job is to decide who will finally win the game if both of them use the best strategy.
输入解释
The input file contains multiply test cases.
The first line of each test case is an integer N (N<100), which represents the number of sub-trees. The following lines show the structure of the trees. The first line of the description of a tree is the number of the nodes m (m<100). The nodes of a tree are numbered from 1 to m. Each of following lines contains 2 integers a and b representing an edge <a, b>. Node 1 is always the root.
The first line of each test case is an integer N (N<100), which represents the number of sub-trees. The following lines show the structure of the trees. The first line of the description of a tree is the number of the nodes m (m<100). The nodes of a tree are numbered from 1 to m. Each of following lines contains 2 integers a and b representing an edge <a, b>. Node 1 is always the root.
输出解释
For each test case, output the name of the winner.
输入样例
2 2 1 2 2 1 2 1 2 1 2
输出样例
PP QQ
来自杭电HDUOJ的附加信息
| Author | alpc27 |
| Recommend | zhouzeyong |
最后修改于 2020-10-25T23:05:02+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码