当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
3589:Jacobi symbol
题目描述
Consider a prime number p and an integer a !≡ 0 (mod p). Then a is called a quadratic residue mod p if there is an integer x such that x2 ≡ a (mod p), and a quadratic non residue otherwise. Lagrange introduced the following notation, called the Legendre symbol, L (a,p):
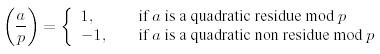
For the calculation of these symbol there are the following rules, valid only for distinct odd prime numbers p, q and integers a, b not divisible by p:
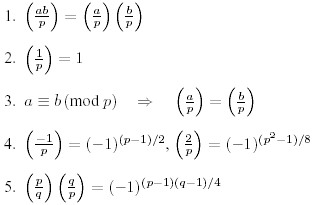
The Jacobi symbol, J (a, n) ,is a generalization of the Legendre symbol ,L (a, p).It defines as :
1. J (a, n) is only defined when n is an odd.
2. J (0, n) = 0.
3. If n is a prime number, J (a, n) = L(a, n).
4. If n is not a prime number, J (a, n) = J (a, p1) *J (a, p2)…* J (a, pm), p1…pm is the prime factor of n.
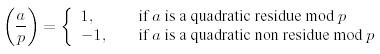
For the calculation of these symbol there are the following rules, valid only for distinct odd prime numbers p, q and integers a, b not divisible by p:
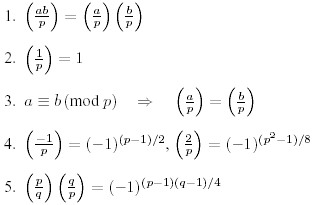
The Jacobi symbol, J (a, n) ,is a generalization of the Legendre symbol ,L (a, p).It defines as :
1. J (a, n) is only defined when n is an odd.
2. J (0, n) = 0.
3. If n is a prime number, J (a, n) = L(a, n).
4. If n is not a prime number, J (a, n) = J (a, p1) *J (a, p2)…* J (a, pm), p1…pm is the prime factor of n.
输入解释
Two integer a and n, 2 < a< =106,2 < n < =106,n is an odd number.
输出解释
Output J (a,n)
输入样例
3 5 3 9 3 13
输出样例
-1 0 1
来自杭电HDUOJ的附加信息
| Author | alpc41 |
| Recommend | zhouzeyong |
最后修改于 2020-10-25T23:05:02+00:00 由爬虫自动更新
共提交 1 次
通过率 100.0%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码