当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
3479:Code
题目描述
A new code system was designed recently. It works in the following way:
The original code A is a linear sequence containing N elements. Each element is an integer between 1 and N. At first the code system will generate a permutation B of length N automatically. Compare sequence A and B we can compute a hidden code C by the following rule:
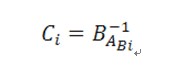
where, B-11 stands for the location of integer i in permutation B. For example, if B = {3, 1, 2}, we have B-11=2,B-13=1 .
The code system has many great advantages in security. For instance, hackers will not have any idea about the original code A if he only gets the hidden code C. Considering all of these, we ordered one of the code systems.
However, some awful thing happened yesterday, the boss totally forgot his original code! The boss has the record of his hidden code, and he wants to ask you if it’s possible for him to find the original code soon.
More exactly, your task is to count the number of possible original codes that may generate the hidden code C by some permutation B.
The original code A is a linear sequence containing N elements. Each element is an integer between 1 and N. At first the code system will generate a permutation B of length N automatically. Compare sequence A and B we can compute a hidden code C by the following rule:
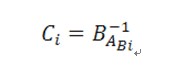
where, B-11 stands for the location of integer i in permutation B. For example, if B = {3, 1, 2}, we have B-11=2,B-13=1 .
The code system has many great advantages in security. For instance, hackers will not have any idea about the original code A if he only gets the hidden code C. Considering all of these, we ordered one of the code systems.
However, some awful thing happened yesterday, the boss totally forgot his original code! The boss has the record of his hidden code, and he wants to ask you if it’s possible for him to find the original code soon.
More exactly, your task is to count the number of possible original codes that may generate the hidden code C by some permutation B.
输入解释
The input contains multiple test cases.
In the first line of the input there’s an integer T which is the number of test cases. Then the description of T test cases will be given.
For each test case there will be two lines. The first line contains one integer N (≤ 30) which is the length of the hidden code C. The second line contains N integers between 1 and N giving C.
In the first line of the input there’s an integer T which is the number of test cases. Then the description of T test cases will be given.
For each test case there will be two lines. The first line contains one integer N (≤ 30) which is the length of the hidden code C. The second line contains N integers between 1 and N giving C.
输出解释
For each test case, output one line containing exactly one integer, the number of different original codes that may generate C. Take a look at the sample output for format.
输入样例
3 5 1 2 3 4 5 5 2 2 2 2 2 5 3 2 5 2 2
输出样例
Case 1: 1 Case 2: 5 Case 3: 120
来自杭电HDUOJ的附加信息
| Recommend | zhengfeng |
最后修改于 2020-10-25T23:03:58+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码