当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
3358:Land Division
题目描述
The king of the Far, Far Away Kingdom has passed-away and the kingdom must be split amongst his K sons. The kingdom, which can be drawn on a rectangular map, consists of N cities. To divide the land, they will draw K-1 straight segments on the map, all of them parallel to either the vertical or the horizontal axis of the map. This divides the map into exactly K rectangles, all having equal heights (if the dividing lines where vertical), or equal widths (if the dividing lines where horizontal). No segment should pass through any of the cities. Each son will then be assigned one random region out of the K regions and the cities inside that region will be his share.
Of course, they want the division to be as fair as possible: theoretically, in the fairest division, each son should get N/K cities (we’ll call this value the baseline), but since the baseline isn’t always a whole number, each of the sons wants to be as close as possible to the baseline. We will calculate the unfairness of each son as the absolute difference between the number of cities assigned to him and the baseline. The fairest division is the one that minimizes the average unfairness of all the sons.
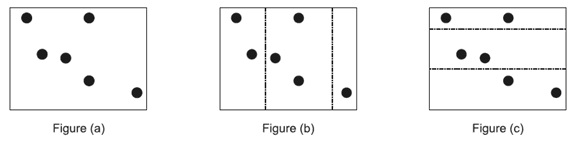
Consider the example above with 3 sons and 6 cities (so the baseline is 6/3 = 2.0) Figure (a) is the original map. Figure (b) shows a non-optimal division (the dashed lines are the 2 dividing lines.) In this case, the middle region contains 3 cities (unfairness of |3 - 2| = 1), the left region contains 1 city (unfairness of |1 - 2| = 1), while the right region contains 2 cities (perfectly fair, unfairness of 0), so the average unfairness is 2/3.
Figure (c) on the right shows the optimal division since all three regions contain the same number of cities for an average unfairness of 0.
Write a program to determine the fairest land division for a given kingdom.
Of course, they want the division to be as fair as possible: theoretically, in the fairest division, each son should get N/K cities (we’ll call this value the baseline), but since the baseline isn’t always a whole number, each of the sons wants to be as close as possible to the baseline. We will calculate the unfairness of each son as the absolute difference between the number of cities assigned to him and the baseline. The fairest division is the one that minimizes the average unfairness of all the sons.

Consider the example above with 3 sons and 6 cities (so the baseline is 6/3 = 2.0) Figure (a) is the original map. Figure (b) shows a non-optimal division (the dashed lines are the 2 dividing lines.) In this case, the middle region contains 3 cities (unfairness of |3 - 2| = 1), the left region contains 1 city (unfairness of |1 - 2| = 1), while the right region contains 2 cities (perfectly fair, unfairness of 0), so the average unfairness is 2/3.
Figure (c) on the right shows the optimal division since all three regions contain the same number of cities for an average unfairness of 0.
Write a program to determine the fairest land division for a given kingdom.
输入解释
Your program will be tested on one or more test cases. Each test case is described on N +1 lines.
The first line of each test case specifies two positive integers: (N <= 100, 000) and (K <= 10) where N is the number of cities and K is number of children. Note that K <= N.
N lines follows, each describing the coordinates of a city by specifying two integers (x, y) where 0 <= x, y <= 100, 000. Since coordinates are rounded to the nearest integer, more than one city could have the exact same coordinate on the map. You may assume that the map of the kingdom is any rectangle that contains all of the given points (although such information is not needed by the program.) Note also that while all cities lie on integer coordinates, the dividing lines need not be.
The last line of the input file contains two zeros.
The first line of each test case specifies two positive integers: (N <= 100, 000) and (K <= 10) where N is the number of cities and K is number of children. Note that K <= N.
N lines follows, each describing the coordinates of a city by specifying two integers (x, y) where 0 <= x, y <= 100, 000. Since coordinates are rounded to the nearest integer, more than one city could have the exact same coordinate on the map. You may assume that the map of the kingdom is any rectangle that contains all of the given points (although such information is not needed by the program.) Note also that while all cities lie on integer coordinates, the dividing lines need not be.
The last line of the input file contains two zeros.
输出解释
For each test case, print the following line:
k. A/B
Where k is the test case number (starting at one,) and A/B is the minimum average that could be obtained. A/B should be an irreducible fraction. Let B=1 when the result is a whole number.
Note: There is a blank space before A.
k. A/B
Where k is the test case number (starting at one,) and A/B is the minimum average that could be obtained. A/B should be an irreducible fraction. Let B=1 when the result is a whole number.
Note: There is a blank space before A.
输入样例
6 3 0 4 1 3 2 3 3 1 4 4 5 0 4 3 0 0 0 1 1 1 1 0 0 0
输出样例
1. 0/1 2. 8/9
来自杭电HDUOJ的附加信息
| Recommend | lcy |
最后修改于 2020-10-25T23:02:42+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码