当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
3330:Here’s a Product Which Will Make You Tensor
题目描述
Most people are familiar with how to multiply two matrices together. However, an alternate form of multiplication known as tensor multiplication exists as well, and works more like you would expect matrix multiplication should. Let A be a p × q matrix and B be an n × m matrix, where neither A nor B is a 1 × 1 matrix. Then the tensor product 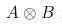 is a pn × qm matrix formed by replacing each element aij in A with the matrix (aij) · B. Two examples are shown below, which also demonstrate that, like normal matrix multiplication, tensor multiplication is non-commutative:
is a pn × qm matrix formed by replacing each element aij in A with the matrix (aij) · B. Two examples are shown below, which also demonstrate that, like normal matrix multiplication, tensor multiplication is non-commutative:

Note that there is no restriction that the number of columns in the first matrix must equal the number of rows in the second, as there is with normal matrix multiplication. The object of this problem is to determine the number of ways (if any) a given matrix can be formed as a result of a tensor multiplication.
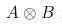 is a pn × qm matrix formed by replacing each element aij in A with the matrix (aij) · B. Two examples are shown below, which also demonstrate that, like normal matrix multiplication, tensor multiplication is non-commutative:
is a pn × qm matrix formed by replacing each element aij in A with the matrix (aij) · B. Two examples are shown below, which also demonstrate that, like normal matrix multiplication, tensor multiplication is non-commutative:
Note that there is no restriction that the number of columns in the first matrix must equal the number of rows in the second, as there is with normal matrix multiplication. The object of this problem is to determine the number of ways (if any) a given matrix can be formed as a result of a tensor multiplication.
输入解释
The first line of input for a test case will contain two positive integers r and c indicating the number of rows and columns in the matrix. After this will follow r lines each containing c positive integers. The values of r and c will be ≤ 500, each entry in the matrix will be no greater than 65,536, and the last test case is followed by a line containing 0 0.
输出解释
For each test case, output the number of different ways the matrix could be the tensor product of two positive integer matrices, neither of which is a 1 × 1 matrix.
输入样例
6 6 1 1 1 2 2 2 1 1 1 2 2 2 1 1 2 2 2 4 3 3 3 4 4 4 3 3 3 4 4 4 3 3 6 4 4 8 2 2 3 6 4 9 2 4 15 18 30 36 20 24 40 48 0 0
输出样例
1 0 4
来自杭电HDUOJ的附加信息
| Recommend | teddy |
最后修改于 2020-10-25T23:02:24+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 4000/2000MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码