当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
3271:SNIBB
题目描述
As we know, some numbers have interesting property. For example, any even number has the property that could be divided by 2. However, this is too simple.
One day our small HH finds some more interesting property of some numbers. He names it the “Special Numbers In Base B” (SNIBB). Small HH is very good at math, so he considers the numbers in Base B. In Base B, we could express any decimal numbers. Let’s define an expression which describe a number’s “SNIBB value”.(Note that all the “SNIBB value” is in Base 10)
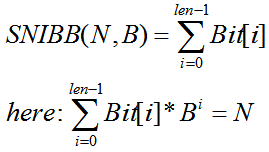
Here N is a non-negative integer; B is the value of Base.
For example, the “SNIBB value” of “1023” in Base “2” is exactly:10
(As we know (1111111111)2=(1023)(10))
Now it is not so difficult to calculate the “SNIBB value” of the given N and B.
But small HH thinks that must be tedious if we just calculate it. So small HH give us some challenge. He would like to tell you B, the “SNIBB value” of N , and he wants you to do two kinds of operation:
1. What is the number of numbers (whose “SNIBB value” is exactly M) in the range [A,B];
2. What it the k-th number whose “SNIBB value” is exactly M in the range [A,B]; (note that the first one is 1-th but not 0-th)
Here M is given.
One day our small HH finds some more interesting property of some numbers. He names it the “Special Numbers In Base B” (SNIBB). Small HH is very good at math, so he considers the numbers in Base B. In Base B, we could express any decimal numbers. Let’s define an expression which describe a number’s “SNIBB value”.(Note that all the “SNIBB value” is in Base 10)
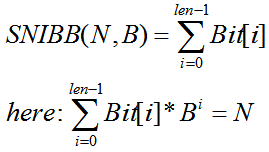
Here N is a non-negative integer; B is the value of Base.
For example, the “SNIBB value” of “1023” in Base “2” is exactly:10
(As we know (1111111111)2=(1023)(10))
Now it is not so difficult to calculate the “SNIBB value” of the given N and B.
But small HH thinks that must be tedious if we just calculate it. So small HH give us some challenge. He would like to tell you B, the “SNIBB value” of N , and he wants you to do two kinds of operation:
1. What is the number of numbers (whose “SNIBB value” is exactly M) in the range [A,B];
2. What it the k-th number whose “SNIBB value” is exactly M in the range [A,B]; (note that the first one is 1-th but not 0-th)
Here M is given.
输入解释
There are no more than 30 cases.
For each case, there is one integer Q,which indicates the mode of operation;
If Q=1 then follows four integers X,Y,B,M, indicating the number is between X and Y, the value of base and the “SNIBB value”.
(0<=X,Y<=2000000000,2<=B<=64,0<=M<=300)
If Q=2 then follows five integers X,Y,B,M,K, the first four integer has the same meaning as above, K indicates small HH want to know the k-th number whose “SNIBB value” is exactly M.
(1<=K<=1000000000)
For each case, there is one integer Q,which indicates the mode of operation;
If Q=1 then follows four integers X,Y,B,M, indicating the number is between X and Y, the value of base and the “SNIBB value”.
(0<=X,Y<=2000000000,2<=B<=64,0<=M<=300)
If Q=2 then follows five integers X,Y,B,M,K, the first four integer has the same meaning as above, K indicates small HH want to know the k-th number whose “SNIBB value” is exactly M.
(1<=K<=1000000000)
输出解释
Output contains two lines for each cases.
The first line is the case number, the format is exactly “Case x:”, here x stands for the case index (start from 1.).
Then follows the answer.
If Q=2 and there is no such number in the range, just output “Could not find the Number!” (without quote!) in a single line.
The first line is the case number, the format is exactly “Case x:”, here x stands for the case index (start from 1.).
Then follows the answer.
If Q=2 and there is no such number in the range, just output “Could not find the Number!” (without quote!) in a single line.
输入样例
1 0 10 10 3 2 0 10 10 1 2 1 0 10 2 1
输出样例
Case 1: 1 Case 2: 10 Case 3: 4
提示
In case 1, the number in the range [0,10] whose “SNIBB value” is exactly 3 is 3(in Base 10); In case 2, the numbers in the range [0,10] whose “SNIBB value” is exactly 1 are 1 and 10; Of course the 2-th number is 10. In case 3, the number in the range [0,10] whose “SNIBB value” is exactly 1 is 1,10,100,1000(in Base 2);
来自杭电HDUOJ的附加信息
| Author | AekdyCoin |
| Recommend | chenheng |
最后修改于 2020-10-25T23:01:50+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码