当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
3246:Special Flow
Special Judge 特殊评判题目描述
There are n junctions numbered from 1 to n, connected by undirected pipes, in which water can flow through. Junction 1 is the source, junction n is the sink. Pipes have capacities, restricting the maximal velocity that water can move through. There will be no water leak, so for every junction (except the source and sink), the amount of water flowing into the junction is equal to the amount of water flowing out of it.
Your task is to find the maximal volume of water that can flow from junction 1 to junction n, during one unit time. Isn’t it the traditional max-flow problem? Well, not exactly. There is an additional restriction in this problem: for an arbitrary pair of junctions u and v, there is a constant S(u,v) such that, in every path from u and v, the sum of water velocity on the arcs along the path is always S(u,v). We calculate the sum in a way such that if the water flows against direction of the path from u to v, its velocity is negated. Note that, for two different pairs (u1,v1) and (u2,v2), S(u,v) may be different from S(u2,v2).
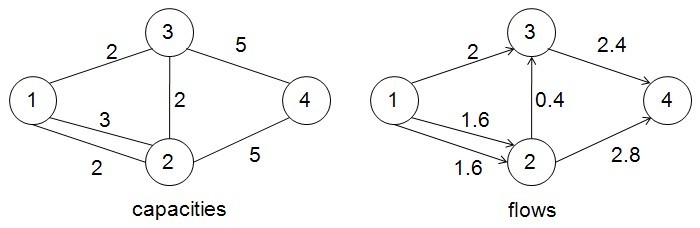
The picture above shows an example pipe network. Capacities of the pipes are shown in the left, while the actual water velocity and flowing directions are shown in the right. You can examine, for example, S(2,4) = 2.8, S(3,1)=-2, S(1,4)=4.4.
Your task is to find the maximal volume of water that can flow from junction 1 to junction n, during one unit time. Isn’t it the traditional max-flow problem? Well, not exactly. There is an additional restriction in this problem: for an arbitrary pair of junctions u and v, there is a constant S(u,v) such that, in every path from u and v, the sum of water velocity on the arcs along the path is always S(u,v). We calculate the sum in a way such that if the water flows against direction of the path from u to v, its velocity is negated. Note that, for two different pairs (u1,v1) and (u2,v2), S(u,v) may be different from S(u2,v2).

The picture above shows an example pipe network. Capacities of the pipes are shown in the left, while the actual water velocity and flowing directions are shown in the right. You can examine, for example, S(2,4) = 2.8, S(3,1)=-2, S(1,4)=4.4.
输入解释
There will be at most 30 test cases. Each case begins with two integers n and m (2 <= n <= 100, 1 <= m <= 5000), the number of junctions and pipes. The next m lines contain the description of pipes. Each pipe is represented by three integers a, b and c, where a and b are the numbers of two different junctions connected by the pipe, and c is the maximal possible water velocity in that pipe (0 <= c <= 10000). The input ends with n = m = 0. There can be multiple pipes between a given pair of junctions.
输出解释
For each test case, print the maximum volume as a floating point number (in any format you like). This number should match the exact result with the maximal absolute difference of 0.0001.
输入样例
4 6 1 3 2 1 2 3 1 2 2 2 4 5 2 3 2 3 4 5 0 0
输出样例
5.2
来自杭电HDUOJ的附加信息
| Recommend | wujianhua |
最后修改于 2020-10-25T23:01:36+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码