当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
3218:Inverse
题目描述
YY and LMY both love mathematics. One day LMY wrote down an integer 3 and two polynomials 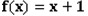 and
and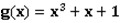 on a piece of paper.
on a piece of paper.
YY noticed that 3 is a prime. Besides, he found that f(x) has a degree strictly less than g(x). And all coefficients of the two polynomials are between 0 and 2,
inclusively. His most important discovery is, that there is a polynomial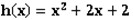 , such that
, such that
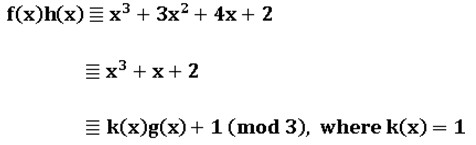
Then YY added a restriction: all coefficients of h(x) must be between 0 and 2 inclusively, and its degree must be less than g(x). Finally, he found that the polynomial
h(x) with such properties is unique.
The property that a polynomial f(x) with all its coefficients between 0 and p-1 inclusively, where p is a prime number, is called that f(x) is in the polynomial ring
defined on field Zp. Note that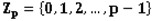 . Such a polynomial ring is called Zp[x].
. Such a polynomial ring is called Zp[x].
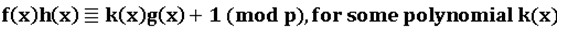
Then h(x) is called a multiplicative inverse of f(x), defined on the quotient ring Zp[x]/(g(x)). YY wonders if such an inverse always exists and is unique.
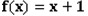 and
and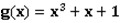 on a piece of paper.
on a piece of paper. YY noticed that 3 is a prime. Besides, he found that f(x) has a degree strictly less than g(x). And all coefficients of the two polynomials are between 0 and 2,
inclusively. His most important discovery is, that there is a polynomial
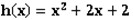 , such that
, such that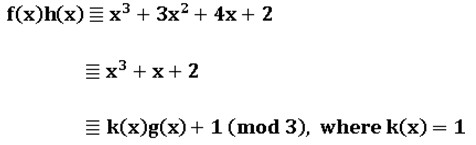
Then YY added a restriction: all coefficients of h(x) must be between 0 and 2 inclusively, and its degree must be less than g(x). Finally, he found that the polynomial
h(x) with such properties is unique.
The property that a polynomial f(x) with all its coefficients between 0 and p-1 inclusively, where p is a prime number, is called that f(x) is in the polynomial ring
defined on field Zp. Note that
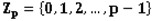 . Such a polynomial ring is called Zp[x].
. Such a polynomial ring is called Zp[x].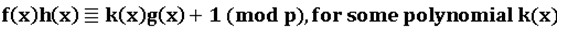
Then h(x) is called a multiplicative inverse of f(x), defined on the quotient ring Zp[x]/(g(x)). YY wonders if such an inverse always exists and is unique.
输入解释
Input contains multiple test cases.
For each test case, the first line contains a prime number p.
The following line consists of two positive integers n and m (n<m), indicating the degrees of f(x) and g(x).
The following line contains n+1 integers, a0, a1… an, indicating the coefficients of f(x), i.e.,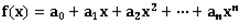 . It is guaranteed that f(x) is
. It is guaranteed that f(x) is
in Zp[x] and an≠0.
The following line contains m+1 integers, b0, b1… bm, indicating the coefficients of g(x), i.e.,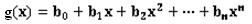 . It is guaranteed that g(x)
. It is guaranteed that g(x)
is in Zp[x] and bm≠0.
Input ends with a line where p=0.
For each test case, the first line contains a prime number p.
The following line consists of two positive integers n and m (n<m), indicating the degrees of f(x) and g(x).
The following line contains n+1 integers, a0, a1… an, indicating the coefficients of f(x), i.e.,
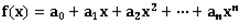 . It is guaranteed that f(x) is
. It is guaranteed that f(x) isin Zp[x] and an≠0.
The following line contains m+1 integers, b0, b1… bm, indicating the coefficients of g(x), i.e.,
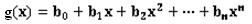 . It is guaranteed that g(x)
. It is guaranteed that g(x)is in Zp[x] and bm≠0.
Input ends with a line where p=0.
输出解释
For each test case, if the multiplicative inverse of f(x) (defined on Zp[x]/(g(x))) does not exist, output only one line containing “NO SOLUTION”(quotes excluded);
if the multiplicative inverse is not unique, output only one line containing “NO UNIQUE SOLUTION”(quotes excluded). Otherwise, you should output two lines
indicating the unique multiplicative inverse h(x), using the same format as in the input.
if the multiplicative inverse is not unique, output only one line containing “NO UNIQUE SOLUTION”(quotes excluded). Otherwise, you should output two lines
indicating the unique multiplicative inverse h(x), using the same format as in the input.
输入样例
2 1 2 0 1 0 0 1 3 1 3 1 1 1 1 0 1 0
输出样例
NO SOLUTION 2 2 2 1
提示
The variable x in a polynomial can be evaluated as anything satisfying the commutative and the associative laws and having the modular p operation, not only members of Zp. So polynomials x2+x and 0 in Z2[x] are different.
来自杭电HDUOJ的附加信息
| Recommend | zhuweicong |
最后修改于 2020-10-25T23:01:16+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码