当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
3210:Another Door Repairing Problem
题目描述
Maybe you have already solved the Door Repairing Problem for YY, who is the officer of the accommodation building B37, in a famous university called Famous University. Maybe you have not, but it does not matter because the new term is coming. So here comes the Another Door Repairing Problem!
As is described in Door Repairing Problem, many students live in B37. The building is old, so sometimes a careless student such as LMY may open the door of the building too vigorously, and break it as a result. However, when a student opens the door and finds it already broken, he will report it to the headmaster, and YY will be punished as a result…
More precisely, the door is fine at the beginning of the term. The term has a length of Tterm. During the term, the door will be opened many times, which can be regarded as a Poisson process, i.e., in any period of length T, the probability that the door will be opened k times is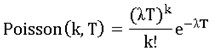 , where λ is a positive real constant.
, where λ is a positive real constant.
Note that for any non-negative real T,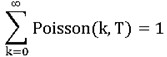
When the door is fine and is opened by some student, the probability that he carelessly breaks the door is p. (0<p<=1) When the door is broken, YY can repair it anytime he likes.
Both repairing the door and being punished cost a lot. YY has thought for many days trying to make a best strategy when to repair the door, so that his expense can be minimized in expectation. He failed, so he is going to try the simplest ways. Given the length of the term Tterm, the constant λ, the probability p, and the question type Q, you are to solve the Another Door Repairing Problem:
When Q=1, tell the expected number of times YY has to repair the door, if he always repairs it immediately after it is broken.
When Q=2, tell the expected number of times YY will be punished, if he never repairs the door.
As is described in Door Repairing Problem, many students live in B37. The building is old, so sometimes a careless student such as LMY may open the door of the building too vigorously, and break it as a result. However, when a student opens the door and finds it already broken, he will report it to the headmaster, and YY will be punished as a result…
More precisely, the door is fine at the beginning of the term. The term has a length of Tterm. During the term, the door will be opened many times, which can be regarded as a Poisson process, i.e., in any period of length T, the probability that the door will be opened k times is
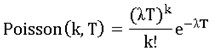 , where λ is a positive real constant.
, where λ is a positive real constant. Note that for any non-negative real T,
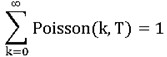
When the door is fine and is opened by some student, the probability that he carelessly breaks the door is p. (0<p<=1) When the door is broken, YY can repair it anytime he likes.
Both repairing the door and being punished cost a lot. YY has thought for many days trying to make a best strategy when to repair the door, so that his expense can be minimized in expectation. He failed, so he is going to try the simplest ways. Given the length of the term Tterm, the constant λ, the probability p, and the question type Q, you are to solve the Another Door Repairing Problem:
When Q=1, tell the expected number of times YY has to repair the door, if he always repairs it immediately after it is broken.
When Q=2, tell the expected number of times YY will be punished, if he never repairs the door.
输入解释
Input contains multiple test cases.
A test case consists of a single line containing four numbers. The first is an integer Q, where Q=1 or Q=2 holds, indicating the type of the problem that you should solve. Three positive real numbers λ, Tterm and p follow. The real numbers may be given in fixed-point or scientific e notations. All real numbers can be store in a double data type of C/C++, with a sufficiently small error rate. See the sample input for details.
Input ends with a line containing four space-separated 0s.
A test case consists of a single line containing four numbers. The first is an integer Q, where Q=1 or Q=2 holds, indicating the type of the problem that you should solve. Three positive real numbers λ, Tterm and p follow. The real numbers may be given in fixed-point or scientific e notations. All real numbers can be store in a double data type of C/C++, with a sufficiently small error rate. See the sample input for details.
Input ends with a line containing four space-separated 0s.
输出解释
For each test case, output one line containing your solution to the specified problem. Your solution should be written in scientific notation: first output a real number, the coefficient part of your solution with two digits after the floating point; then output one space; then output an integer, the exponential part of your solution. You may assume that the absolute value of the exponential part is less than 100. See sample output for details.
输入样例
1 1 1 0.5 1 1 1 1e0 2 1 1 5.00000e-0001 0 0 0 0
输出样例
5.00 -1 1.00 0 2.13 -1
提示
The solution to sample input is 0.5, 1.0 and 0.213, respectively. Don’t worry about inputting real numbers in scientific e notations. A simple scanf or cin as if it is fixed-point is OK.
来自杭电HDUOJ的附加信息
| Recommend | zhuweicong |
最后修改于 2020-10-25T23:01:12+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码