当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
3163:Meltdown
题目描述

A polygon is lowered at a constant speed of v metres per minute from the air into a liquid that dissolves it at a constant speed of c metres per minute from all sides. Given a point (x,y) inside the polygon that moves with the polygon, determine when the liquid reaches the point.
The border between air and liquid always has y-coordinate 0, and the liquid only eats away from the sides of the polygon in 2 dimensions. The polygon does not rotate as it is lowered into the liquid, and at time 0, it is not touching the liquid.
Unlike the polygon, which is flat (2-dimensional), the liquid exists in three dimensions. Therefore, the liquid seeps into cavities in the polygon. For example, if the polygon is "cup-shaped", the liquid can get "inside" the cup, as in the diagram below.
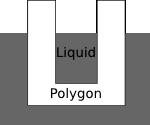
输入解释
The input consists of several test cases.
The first line of each test case contains the five integers N, x, y, v, and c, where 3 <= N <= 30, -100 <= x <= 100, 1 <= y <= 100, and 1 <= c < v <= 10.
The following N lines of the test case each contain one vertex of the polygon. The ith line contains the two integers x, y, where -100 <= x <= 100, 1 <= y <= 100.
The vertices of the polygon are given in counter-clockwise order. The border of the polygon does not intersect or touch itself, and the point (x,y) lies strictly inside the polygon--it does not lie on the border of the polygon.
Input is terminated by a line containing 0 0 0 0 0. These zeros are not a test case and should not be processed.
The first line of each test case contains the five integers N, x, y, v, and c, where 3 <= N <= 30, -100 <= x <= 100, 1 <= y <= 100, and 1 <= c < v <= 10.
The following N lines of the test case each contain one vertex of the polygon. The ith line contains the two integers x, y, where -100 <= x <= 100, 1 <= y <= 100.
The vertices of the polygon are given in counter-clockwise order. The border of the polygon does not intersect or touch itself, and the point (x,y) lies strictly inside the polygon--it does not lie on the border of the polygon.
Input is terminated by a line containing 0 0 0 0 0. These zeros are not a test case and should not be processed.
输出解释
For each test case, output the first time in minutes that the liquid reaches the specified point, rounded to four decimal places.
输入样例
4 0 50 2 1 -1 10 1 10 1 90 -1 90 0 0 0 0 0
输出样例
25.8660
来自杭电HDUOJ的附加信息
| Recommend | chenrui |
最后修改于 2020-10-25T23:00:48+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码