当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
3027:Network
题目描述
There is a network which is a completely binary tree. In the network, there are 2N users numbered from 1, 2, 3, 4, ... 2N, which are the leaves in the network-tree. For example, Figure 1 is a network-tree. In the tree, there are 8 users (leaf nodes) and 7 transmitters (gray nodes).
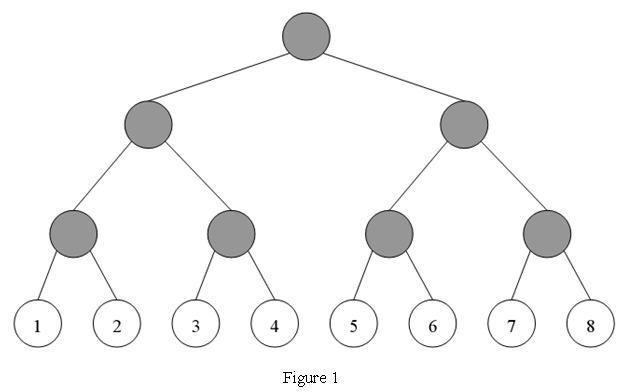
Using network-tree means that you have to pay a cost for it. The charging way is so interesting, named "pair charging". The cost you must pay is the sum of cost from every pair of user i and user j ( 1 ≤ i < j ≤ 2N). Every user can choose mode A or mode B to pay for the charge.
For every two users i, j (1 ≤ i < j ≤ 2N), first find their LCA (The Least Common Ancestors): Transmitter P. Then count the number of mode A users in the tree of ROOT transmitter P, so do mode B.
Next, let's name the number nA and nB and at last charge the cost.
f[i][j] is the flow between user i and user j.
The charging way is followed:
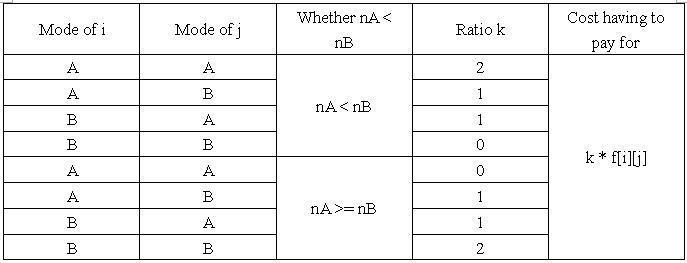
At first, every user has an initial mode, A or B. However, they want to reduce the cost, so a part of them would change the mode from A to B, or from B to A. Every change will have an extra cost. If user i changes his mode, he will pay Ci cost.
Now, you should find the minimum cost, that is, the sum of the cost having to pay for and the extra cost of changing mode.

Using network-tree means that you have to pay a cost for it. The charging way is so interesting, named "pair charging". The cost you must pay is the sum of cost from every pair of user i and user j ( 1 ≤ i < j ≤ 2N). Every user can choose mode A or mode B to pay for the charge.
For every two users i, j (1 ≤ i < j ≤ 2N), first find their LCA (The Least Common Ancestors): Transmitter P. Then count the number of mode A users in the tree of ROOT transmitter P, so do mode B.
Next, let's name the number nA and nB and at last charge the cost.
f[i][j] is the flow between user i and user j.
The charging way is followed:

At first, every user has an initial mode, A or B. However, they want to reduce the cost, so a part of them would change the mode from A to B, or from B to A. Every change will have an extra cost. If user i changes his mode, he will pay Ci cost.
Now, you should find the minimum cost, that is, the sum of the cost having to pay for and the extra cost of changing mode.
输入解释
First line, an integer N (N ≤ 10).
Sencond line, 2N integers, ith integer stands for ith user's initial mode. 0 is mode A, 1 is mode B.
Third line, 2N integers, ith integer stands for Ci, the cost that ith user changes his mode. (0 ≤ Ci ≤ 500 000)
Next 2N - 1 line, describe the flow of every pair of users. The i + 3 th line's (in the whole input) j row's integer standing for the f[i][j + i]. (1 ≤ i ≤ 2^N ,1 ≤ j ≤ 2^N - i, 0 ≤ f[i][j] ≤ 500).
Sencond line, 2N integers, ith integer stands for ith user's initial mode. 0 is mode A, 1 is mode B.
Third line, 2N integers, ith integer stands for Ci, the cost that ith user changes his mode. (0 ≤ Ci ≤ 500 000)
Next 2N - 1 line, describe the flow of every pair of users. The i + 3 th line's (in the whole input) j row's integer standing for the f[i][j + i]. (1 ≤ i ≤ 2^N ,1 ≤ j ≤ 2^N - i, 0 ≤ f[i][j] ≤ 500).
输出解释
Only a single integer, standing for the minimum cost above.
输入样例
2 1 0 1 0 2 2 10 9 10 1 2 2 1 3
输出样例
8 Explanation: Changing the user 1's mode from B to A will minimumize the cost.
来自杭电HDUOJ的附加信息
| Recommend | gaojie |
最后修改于 2020-10-25T22:59:21+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/10000MS(Java/Others) | 98304/98304K(Java/Others) |
登陆或注册以提交代码