当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
2977:Color Squares
题目描述
You have a 3 * 3 board of color squares. Each square is either empty or has a block in it. Initially, all the squares are empty. There are four kinds of blocks: blue (B), red (R), green (G) and yellow (Y). Each of these block scores wb, wr, wg and wy , respectively (blocks of the same color always have the same score). We assume that wb<=wr<=wg<=wy .
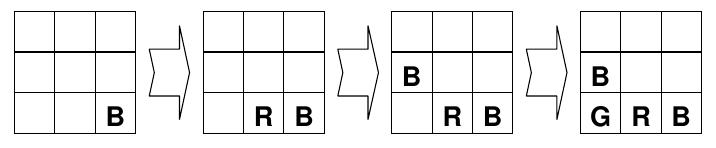
In each step, you can place a new block in a square. If that square already has a block in it, take it out first (taking it out does not count as a step). You can do this as many times as you like (you're given enough blocks for each color), as long as you follow these rules:
Rule 1: You can always place a blue block.
Rule 2: You can place a red block if and only if it's surrounded by at least one blue block.
Rule 3: You can place a green block if and only if it's surrounded by at least one blue and one red block.
Rule 4: You can place a yellow block if and only if it's surrounded by at least one blue, one red and one green block
Every square is surrounded by squares that share one edge with it, so each of four corner squares is surrounded by exactly two squares, each of four squares on the edge (but not at corners) is surrounded by exactly three squares, and the center square is surrounded by exactly four squares.
Write a program to find the minimal number of steps needed to get a score of at least w . The total score is the sum of individual scores of each block on the current board, regardless of what blocks you've thrown away.

In each step, you can place a new block in a square. If that square already has a block in it, take it out first (taking it out does not count as a step). You can do this as many times as you like (you're given enough blocks for each color), as long as you follow these rules:
Rule 1: You can always place a blue block.
Rule 2: You can place a red block if and only if it's surrounded by at least one blue block.
Rule 3: You can place a green block if and only if it's surrounded by at least one blue and one red block.
Rule 4: You can place a yellow block if and only if it's surrounded by at least one blue, one red and one green block
Every square is surrounded by squares that share one edge with it, so each of four corner squares is surrounded by exactly two squares, each of four squares on the edge (but not at corners) is surrounded by exactly three squares, and the center square is surrounded by exactly four squares.
Write a program to find the minimal number of steps needed to get a score of at least w . The total score is the sum of individual scores of each block on the current board, regardless of what blocks you've thrown away.
输入解释
The input contains several test cases. Each case contains five positive integer, wb, wr, wg, wy, w (1<=wb<=wr<=wg<=wy≤100, 0<=w<=1000) in a single line. The last test case is followed by a single zero, which should not be processed.
输出解释
For each test case, print the case number and the minimum number of steps. If it is impossible, output ``Impossible".
输入样例
1 1 1 1 3 1 2 4 8 21 1 1 1 100 500 7 20 53 94 395 0
输出样例
Case 1: 3 Case 2: 7 Case 3: Impossible Case 4: 11
来自杭电HDUOJ的附加信息
| Recommend | gaojie |
最后修改于 2020-10-25T22:58:50+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码