当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
2976:Bricks
题目描述
You have some equal-height bricks and want to pile them into a two-layered object. To ensure the stability of the object, no full half-blocks can be over empty space. There are totally four half-blocks for each brick, shown below.

The following figure shows an object consisting of four 2 * 2 * h bricks in the lower layer, one 2 * 2 * h brick in the upper layer. Each half-block does not include its boundary, so you're not allowed to leave only one brick, since the upper brick would have two half-blocks hanging over empty space (though you may argue that the upper brick may stand still if you don't touch it). In this case, at most 2 bricks could be removed.
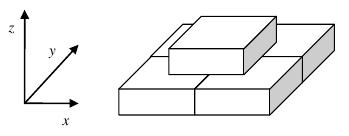
Each time, you can remove exactly one brick from the lower layer by dragging it in one of four possible directions: decreasing x (left), increasing x (right), decreasing y (front), increasing y (back). You can only drag a brick along one direction. E.g. you cannot drag it to the left, and then to the front to remove it. The bricks are smooth enough and don't suffer from fraction, so you can remove any brick you want as long as dragging it out does not hit any other brick (touching other bricks is allowed, though), and after the brick is removed, no full half-blocks of any brick in upper layer are over empty space.
Write a program to find the maximum number of bricks you can remove from the lower layer.

The following figure shows an object consisting of four 2 * 2 * h bricks in the lower layer, one 2 * 2 * h brick in the upper layer. Each half-block does not include its boundary, so you're not allowed to leave only one brick, since the upper brick would have two half-blocks hanging over empty space (though you may argue that the upper brick may stand still if you don't touch it). In this case, at most 2 bricks could be removed.

Each time, you can remove exactly one brick from the lower layer by dragging it in one of four possible directions: decreasing x (left), increasing x (right), decreasing y (front), increasing y (back). You can only drag a brick along one direction. E.g. you cannot drag it to the left, and then to the front to remove it. The bricks are smooth enough and don't suffer from fraction, so you can remove any brick you want as long as dragging it out does not hit any other brick (touching other bricks is allowed, though), and after the brick is removed, no full half-blocks of any brick in upper layer are over empty space.
Write a program to find the maximum number of bricks you can remove from the lower layer.
输入解释
The input contains several test cases. The first line of input contains two integer m, n (1<=m, n<=10) , the number of bricks in the lower and upper layer. The next line describes the lower layer with m brick descriptions in format (x1, y1) - (x2, y2) where integers x1, y1, x2, y2 do not exceed 1000 by their absolute values and they satisfy x1 < x2, y1 < y2 . Each description does not contain any space inside; neighboring descriptions are separated by exactly one single space. The next line describes the upper layer in the same format. The initial object is always valid. The last test case is followed by a single zero, which should not be processed.
输出解释
For each test case, print the case number and the number of bricks can be removed from the lower layer.
输入样例
1 1 (0,0)-(1,1) (0,0)-(1,1) 4 1 (0,0)-(2,2) (2,0)-(4,2) (0,2)-(2,4) (2,2)-(4,4) (1,1)-(3,3) 0
输出样例
Case 1: 0 Case 2: 2
来自杭电HDUOJ的附加信息
| Recommend | gaojie |
最后修改于 2020-10-25T22:58:49+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 4000/2000MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码