当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
2950:Communication Channels
题目描述
Classical information theory is based on the concept of a communication channel.
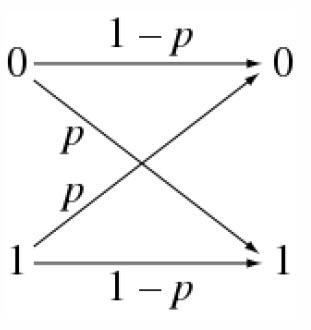
Information theory is generally considered to have been founded in 1948 by Claude Shan-non in his seminal work, \A Mathemati-cal Theory of Communication." The cen-tral paradigm of classical information theory is the engineering problem of the transmis-sion of information over a noisy channel. http://en.wikipedia.org/wiki/Information theory
In this problem, we will specifically consider one of the simplest possible noisy channels, namely the binary symmetric channel (BSC). A BSC transmits a sequence of bits, but each transmitted bit has a probability p of being fiipped to the wrong bit. This is called the crossover probability, as can be understood from the figure. We assume independent behaviour on difierent bits, so a communication of l bits has probability (1 - p)^l of being transmitted
correctly. Note that one can always assume that p < 1/2, since a channel with p = 1/2 is totally useless, and a channel with p > 1/2 can easily be transformed to a new channel having crossover probability 1 - p by just flipping all bits of the output.
Of course, it is still possible to communicate over a noisy channel. (In fact, you are doing it all the time!) To be able to do this, one has to add extra bits in order for the receiver to detect or even possibly correct errors. Example implementations of such a feature are parity bits, Cyclic Redundancy Checks (CRC) and Golay codes.
These are not relevant to this problem, however, so they will not be discussed here.
In this problem you must investigate the behaviour of a binary symmetric channel.

Information theory is generally considered to have been founded in 1948 by Claude Shan-non in his seminal work, \A Mathemati-cal Theory of Communication." The cen-tral paradigm of classical information theory is the engineering problem of the transmis-sion of information over a noisy channel. http://en.wikipedia.org/wiki/Information theory
In this problem, we will specifically consider one of the simplest possible noisy channels, namely the binary symmetric channel (BSC). A BSC transmits a sequence of bits, but each transmitted bit has a probability p of being fiipped to the wrong bit. This is called the crossover probability, as can be understood from the figure. We assume independent behaviour on difierent bits, so a communication of l bits has probability (1 - p)^l of being transmitted
correctly. Note that one can always assume that p < 1/2, since a channel with p = 1/2 is totally useless, and a channel with p > 1/2 can easily be transformed to a new channel having crossover probability 1 - p by just flipping all bits of the output.
Of course, it is still possible to communicate over a noisy channel. (In fact, you are doing it all the time!) To be able to do this, one has to add extra bits in order for the receiver to detect or even possibly correct errors. Example implementations of such a feature are parity bits, Cyclic Redundancy Checks (CRC) and Golay codes.
These are not relevant to this problem, however, so they will not be discussed here.
In this problem you must investigate the behaviour of a binary symmetric channel.
输入解释
The first line of the input consists of a single number T, the number of transmissions.
Then follow T lines with the input and the output of each transmission as binary strings, separated by a single space.
Then follow T lines with the input and the output of each transmission as binary strings, separated by a single space.
输出解释
For each transmission, output OK if the communication was transmitted correctly, or ERROR if it was transmitted incorrectly.
Notes and Constraints
0 < T <= 100
All inputs and outputs has length less than 120.
T is encoded in decimal.
Notes and Constraints
0 < T <= 100
All inputs and outputs has length less than 120.
T is encoded in decimal.
输入样例
2 10 10 10 11
输出样例
OK ERROR
来自杭电HDUOJ的附加信息
| Recommend | gaojie |
最后修改于 2020-10-25T22:58:34+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码