当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
2928:A Rod in a Path
题目描述
Alice has a rod. One day, she draws a path on a grid and puts the rod on it. The path begins at (0, 0) and continues to the right. The first and last segments are always horizontal, so there are always an odd number of segments. If we number the segments 1, 2, … , n, odd-numbered segments are all horizontal, while other segments (if any) are vertical. Initially, one endpoint B of the rod is located at (0, 0), and the other endpoint A is at (L, 0), where L is the length of the rod. The length of the first segment is at least L. When moving the rod, both endpoints A and B must be always on the path, though other parts may be outside. The rod is hard, so its length (i.e. distance between A and B) is always L.
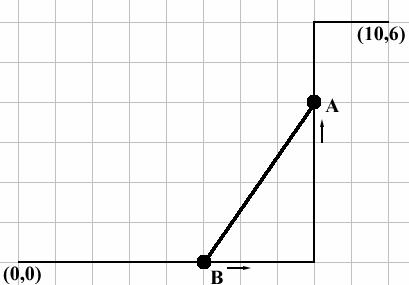
Write a program to compute the minimum distance A must cover to reach the rightmost endpoint of the path.

Write a program to compute the minimum distance A must cover to reach the rightmost endpoint of the path.
输入解释
The input consists of several test cases. The first line of each case contains two integers n and L (1 ≤ n ≤ 10, 1 ≤ L ≤ 30),described above. The second line contains n non-zero integers li (-30 ≤ li ≤ 30), the lengths and directions of path segments. The absolute value of li denotes length of the i-th segment. If it is horizontal, li is positive. That means, horizontal segments are always left-to-right. If it is vertical, positive means down-to-up (increasing y coordinate), negative means up-to-down (decreasing y coordinate). The last test case is followed by a single zero, which should not be processed.
输出解释
For each test case, print the case number and the minimum distance to two decimal places. If it's not possible to reach the rightmost point, print -1.
输入样例
3 5 8 6 2 5 2 3 1 1 -4 1 0
输出样例
Case 1: 11.00 Case 2: 10.00
来自杭电HDUOJ的附加信息
| Recommend | lcy |
最后修改于 2020-10-25T22:58:18+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码