当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
2919:Adding Sevens
题目描述
A seven segment display, similar to the one shown on the right, is composed of seven light-emitting elements. Individually on or off, they can be combined to produce 127 different combinations, including the ten Arabic numerals. The figure below illustrates how the ten numerals are displayed.

7-seg displays (as they're often abbreviated) are widely used in digital clocks, electronic meters, and calculators.
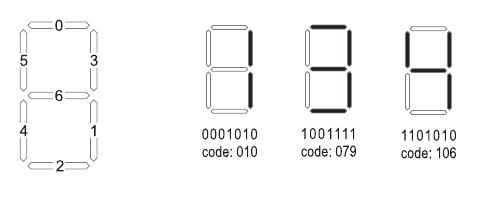
A 7-seg has seven connectors, one for each element, (plus few more connectors for other electrical purposes.) Each element can be turned on by sending an electric current through its pin. Each of the seven pins is viewed by programmers as a single bit in a 7-bit number, as they are more comfortable dealing with bits rather than electrical signals. The figure below shows the bit assignment for a typical 7-seg, bit 0 being the right-most bit.
For example, in order to display the digit 1, the programmer knows that only bits 1 and 3 need to be on, i.e. the 7-bit binary number to display digit 1 is ``0001010", or 10 in decimal. Let's call the decimal number for displaying a digit, its display code, or just code for short. Since a 7-seg displays 127 different configurations, display codes are normally written using 3 decimal places with leading zeros if necessary, i.e. the display code for digit 1 is written as 010.
In a 9-digit calculator, 9 7-seg displays are stacked next to each other, and are all controlled by a single controller. The controller is sent a sequence of 3n digits, representing n display codes, where 0 < n < 10 . If n < 9 , the number is right justified and leading zeros are automatically displayed. For example, the display code for 13 is 010079 while for 144 it is 010106106
Write a program that reads the display codes of two numbers, and prints the display code of their sum.

7-seg displays (as they're often abbreviated) are widely used in digital clocks, electronic meters, and calculators.

A 7-seg has seven connectors, one for each element, (plus few more connectors for other electrical purposes.) Each element can be turned on by sending an electric current through its pin. Each of the seven pins is viewed by programmers as a single bit in a 7-bit number, as they are more comfortable dealing with bits rather than electrical signals. The figure below shows the bit assignment for a typical 7-seg, bit 0 being the right-most bit.
For example, in order to display the digit 1, the programmer knows that only bits 1 and 3 need to be on, i.e. the 7-bit binary number to display digit 1 is ``0001010", or 10 in decimal. Let's call the decimal number for displaying a digit, its display code, or just code for short. Since a 7-seg displays 127 different configurations, display codes are normally written using 3 decimal places with leading zeros if necessary, i.e. the display code for digit 1 is written as 010.
In a 9-digit calculator, 9 7-seg displays are stacked next to each other, and are all controlled by a single controller. The controller is sent a sequence of 3n digits, representing n display codes, where 0 < n < 10 . If n < 9 , the number is right justified and leading zeros are automatically displayed. For example, the display code for 13 is 010079 while for 144 it is 010106106
Write a program that reads the display codes of two numbers, and prints the display code of their sum.
输入解释
Your program will be tested on one or more test cases. Each test case is specified on a single line in the form of A +B = where both A and B are display codes for decimal numbers a and b respectively where 0 < a , b < a + b < 1, 000, 000, 000 . The last line of the input file is the word ``BYE'' (without the double quotes.)
输出解释
For each test case, print A +B =C where C is the display code for a + b .
输入样例
010079010+010079= 106010+010= BYE
输出样例
010079010+010079=010106106 106010+010=106093
来自杭电HDUOJ的附加信息
| Recommend | lcy |
最后修改于 2020-10-25T22:58:12+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 2000/1000MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码