当前你的浏览器版本过低,网站已在兼容模式下运行,兼容模式仅提供最小功能支持,网站样式可能显示不正常。
请尽快升级浏览器以体验网站在线编辑、在线运行等功能。
2917:Zigzag
Special Judge 特殊评判题目描述
Given several points on a plane, let’s try to solve a puzzle connecting them with a zigzag line.
The puzzle is to find the zigzag line that passes through all the given points with the minimum number of turns. Moreover, when there are several zigzag lines with the minimum number of turns, the shortest one among them should be found.
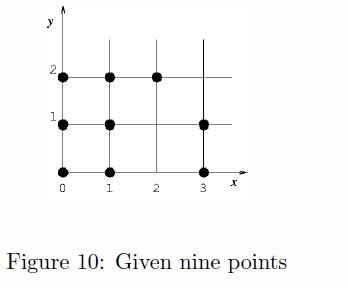
For example, consider nine points given in Figure 10.
A zigzag line is composed of several straight line segments. Here, the rule requests that each line segment should pass through two or more given points.
A zigzag line may turn at some of the given points or anywhere else. There may be some given points passed more than once.
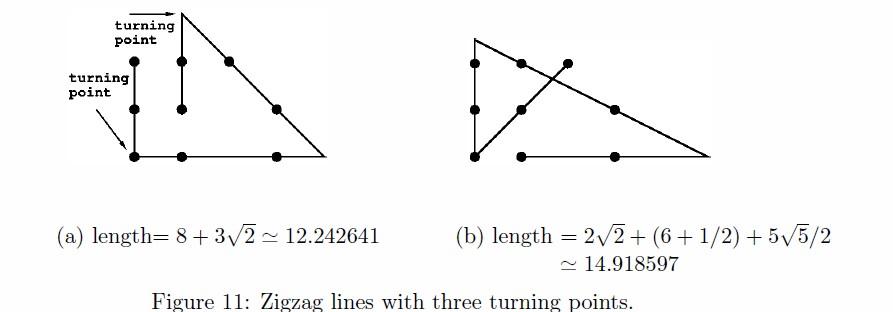
Two zigzag lines with three turning points are depicted in Figure 11 (a) and (b) for the same set of given points shown in Figure 10. The length of the zigzag line in Figure 11 (a) is shorter than that in Figure 11 (b). In fact, the length of the zigzag line in Figure 11 (a) is shortest so that it is the solution for the nine points given in Figure 10.
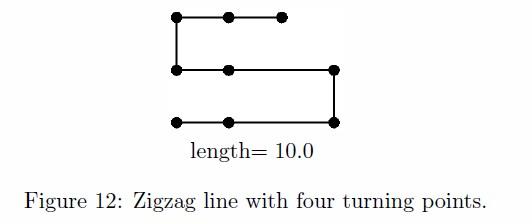
Another zigzag line with four turning points is depicted in Figure 12. Its length is shorter than those in Figure 11, however, the number of turning points is greater than those in Figure 11, and thus, it is not the solution.
There are two zigzag lines that passes another set of given points depicted in Figure 13 (a) and (b).
Both have the same number of turning points, and the line in (a) is longer than that in (b). However, the solution is (a), because one of the segments of the zigzag line in (b) passes only one given point, violating the rule.

Your job is to write a program that solves this puzzle.
The puzzle is to find the zigzag line that passes through all the given points with the minimum number of turns. Moreover, when there are several zigzag lines with the minimum number of turns, the shortest one among them should be found.

For example, consider nine points given in Figure 10.
A zigzag line is composed of several straight line segments. Here, the rule requests that each line segment should pass through two or more given points.
A zigzag line may turn at some of the given points or anywhere else. There may be some given points passed more than once.

Two zigzag lines with three turning points are depicted in Figure 11 (a) and (b) for the same set of given points shown in Figure 10. The length of the zigzag line in Figure 11 (a) is shorter than that in Figure 11 (b). In fact, the length of the zigzag line in Figure 11 (a) is shortest so that it is the solution for the nine points given in Figure 10.
Another zigzag line with four turning points is depicted in Figure 12. Its length is shorter than those in Figure 11, however, the number of turning points is greater than those in Figure 11, and thus, it is not the solution.

There are two zigzag lines that passes another set of given points depicted in Figure 13 (a) and (b).
Both have the same number of turning points, and the line in (a) is longer than that in (b). However, the solution is (a), because one of the segments of the zigzag line in (b) passes only one given point, violating the rule.

Your job is to write a program that solves this puzzle.
输入解释
The input consists of multiple datasets, followed by a line containing one zero. Each dataset has the following format.
n
x1 y1
...
xn yn
Every input item in a dataset is a non-negative integer. Items in a line are separated by a single space. n is the number of the given points. xk and yk (k = 1,.... n) indicate the position of the k-th point. The order of the points is meaningless. You can assume that 2 ≤ n ≤ 10, 0 ≤ xk ≤ 10, and 0 ≤ yk ≤ 10.
n
x1 y1
...
xn yn
Every input item in a dataset is a non-negative integer. Items in a line are separated by a single space. n is the number of the given points. xk and yk (k = 1,.... n) indicate the position of the k-th point. The order of the points is meaningless. You can assume that 2 ≤ n ≤ 10, 0 ≤ xk ≤ 10, and 0 ≤ yk ≤ 10.
输出解释
For each dataset, the minimum number of turning points and the length of the shortest zigzag line with that number of turning points should be printed, separated by a space in a line. The length should be in a decimal fraction with an error less than 0.0001 (= 1:0 * 10-4). You may assume that the minimum number of turning points is at most four, that is, the number of line segments is at most five.
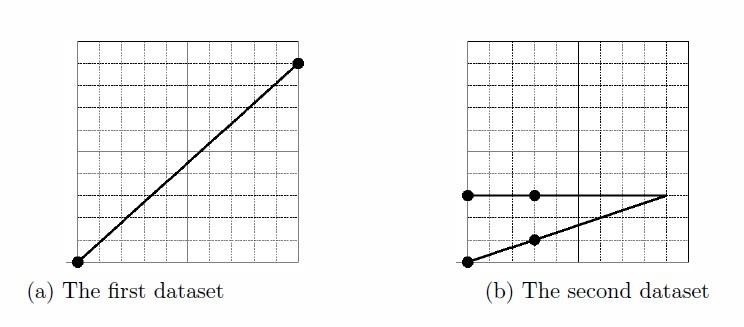
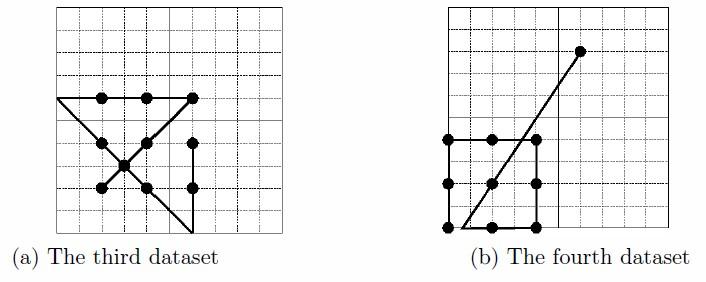
The example solutions for the first four datasets in the sample input are depicted in Figure 14 and 15.
The example solutions for the first four datasets in the sample input are depicted in Figure 14 and 15.
输入样例
2 0 0 10 9 4 0 0 3 1 0 3 3 3 10 2 2 4 2 6 2 2 4 4 4 6 4 2 6 4 6 6 6 3 3 10 0 0 2 0 4 0 0 2 2 2 4 2 0 4 2 4 4 4 6 8 9 0 0 1 0 3 0 0 1 1 1 3 1 0 2 1 2 2 2 10 0 0 1 0 0 1 1 1 9 9 9 10 10 9 10 10 0 2 10 8 10 0 0 0 10 2 0 2 1 2 7 2 10 5 1 6 7 9 2 10 9 0
输出样例
0 13.45362405 1 18.48683298 3 24.14213562 4 24.94813673 3 12.24264069 3 60.78289622 3 502.7804353
提示
Figure 14: Example solutions for the first and the second datasets in the sample inputs. Figure 15: Example solutions for the third and the fourth datasets in the sample inputs.
来自杭电HDUOJ的附加信息
| Recommend | lcy |
最后修改于 2020-10-25T22:58:09+00:00 由爬虫自动更新
共提交 0 次
通过率 --%
| 时间上限 | 内存上限 |
| 15000/10000MS(Java/Others) | 32768/32768K(Java/Others) |
登陆或注册以提交代码